某班同学利用国庆节进行社会实践，对
岁的人群随机抽取
人
进行了一次生活习惯是否符合低碳观念的调查，若生活习惯符合低碳观念的称为“低碳族”，
否则称为“
非低碳族”，得到如下
统计表和各年龄段人数频率分布直方图：
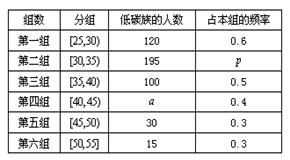
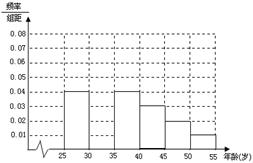
（1）补全频率分布直方图并求、
、
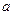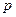的值；
（2）从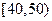
岁年龄段的“低碳族”中采用分层抽样法抽取
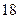人参加户外低碳体验活动，其中选取
人作为领队，记选取的名领队中年龄在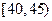
岁的人数为
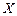，求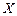的分布列和期望
．
（本题14分）已知直线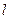
：y=kx+1与双曲线C：2x2-y2=1的右支交于不同的两点A、B。（1）求实数k的取值范围；（2）是否存在实数k，使得以线段AB为直径的圆经过双曲线C的右焦点F？若荐在，求出k的值。若不存在，说明理由。
（本题12分）某研究所计划利用“神七”宇宙飞船进行新产品搭载实验，计划搭载新产品A、B，该所要根据该产品的研制成本、产品重量、搭载实验费用和预计产生收益来决定具体安排，通过调查，有关数据如下表：
| 产品A（件） |
产品B（件） |
||
| 研制成本、搭载费用之和（万元） |
20 |
30 |
计划最大资金额300万元 |
| 产品重量（千克） |
10 |
5 |
最大搭载重量110千克 |
| 预计收益（万元） |
80 |
60 |
如何安排这两种产品的件数进行搭载，才能使总预计收益达到最大，最大收益是多少？
（本题12分）在如图所示的四面体ABCD中，AB、BC、CD两两互相垂直，且BC=CD=1。（1）求证：平面ACD⊥平面ABC；（2）求二面角C-AB-D的大小。
（本题12分）已知命题p：|4-x|≤6，q：x2-2x+1- a2≥0（a>0），若非p是q的充分不必要条件，求a的取值范围。
（本题12分）在锐角△ABC中，a，b，c分别为角A、B、C所对的边，且
a=2csinA,（1）确定角C的大小；（2）若c=
，且△ABC的面积为
，求a+b的值。