已知函数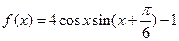 .
.
(1)求 的最小正周期;
的最小正周期;
(2)求 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
已知矩阵 =
= ,求
,求 的特征值
的特征值 ,
, 及对应的特征向量
及对应的特征向量 .
.
(本小题16分)
已知函数 ,
, 为正常数。
为正常数。
(1)若 ,且
,且 ,求函数
,求函数 的单调增区间;
的单调增区间;
(2)若 ,且对任意
,且对任意 ,
, ,都有
,都有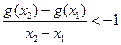 ,求
,求 的的取值范围。
的的取值范围。
(本小题16分)
已知数列 满足:
满足: (
( 为常数),数列
为常数),数列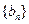 中,
中,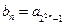 。
。
(1)求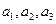 ;
;
(2)证明:数列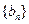 为等差数列;
为等差数列;
(3)求证:数列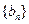 中存在三项构成等比数列时,
中存在三项构成等比数列时, 为有理数。
为有理数。
(本小题16分)
已知抛物线的顶点在坐标原点,对称轴为 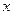 轴,焦点
轴,焦点  在直线
在直线  上,直线
上,直线  与抛物线相交于
与抛物线相交于  两点,
两点,  为抛物线上一动点(不同于
为抛物线上一动点(不同于  ),直线
),直线  分别交该抛物线的准线
分别交该抛物线的准线  于点
于点  。
。
(1)求抛物线方程;
(2)求证:以  为直径的圆
为直径的圆  经过焦点
经过焦点  ,且当
,且当  为抛物线的顶点时,圆
为抛物线的顶点时,圆  与直线
与直线  相切。
相切。 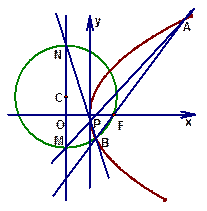
(本小题14分)
已知某种稀有矿石的价值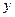 (单位:元)与其重量
(单位:元)与其重量 (单位:克)的平方成正比,且
(单位:克)的平方成正比,且 克该种矿石的价值为
克该种矿石的价值为 元。
元。
(1)写出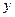 (单位:元)关于
(单位:元)关于 (单位:克)的函数关系式;
(单位:克)的函数关系式;
(2)若把一块该种矿石切割成重量比为 的两块矿石,求价值损失的百分率;
的两块矿石,求价值损失的百分率;
(3)把一块该种矿石切割成两块矿石时,切割的重量比为多少时,价值损失的百分率最大。(注:价值损失的百分率 ;在切割过程中的重量损耗忽略不计)
;在切割过程中的重量损耗忽略不计)