(本小题14分)
已知某种稀有矿石的价值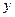 (单位:元)与其重量
(单位:元)与其重量 (单位:克)的平方成正比,且
(单位:克)的平方成正比,且 克该种矿石的价值为
克该种矿石的价值为 元。
元。
(1)写出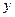 (单位:元)关于
(单位:元)关于 (单位:克)的函数关系式;
(单位:克)的函数关系式;
(2)若把一块该种矿石切割成重量比为 的两块矿石,求价值损失的百分率;
的两块矿石,求价值损失的百分率;
(3)把一块该种矿石切割成两块矿石时,切割的重量比为多少时,价值损失的百分率最大。(注:价值损失的百分率 ;在切割过程中的重量损耗忽略不计)
;在切割过程中的重量损耗忽略不计)
已知函数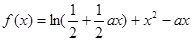 。(
。( 为常数,
为常数,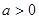 )
)
(Ⅰ)若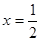 是函数
是函数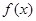 的一个极值点,求
的一个极值点,求 的值;
的值;
(Ⅱ)求证:当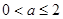 时,
时,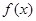 在
在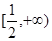 上是增函数;
上是增函数;
(Ⅲ)若对任意的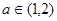 ,总存在
,总存在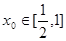 ,使不等式
,使不等式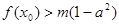 成立,求实数
成立,求实数 的取值范围。
的取值范围。
已知数列 满足
满足 ,
, ,
,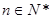 ,且
,且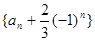 是等比数列。
是等比数列。
(Ⅰ)求 的值;
的值;
(Ⅱ)求出通项公式 ;
;
(Ⅲ)求证: …
…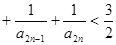
在股票市场上,投资者常参考股价(每一股的价格)的某条平滑均线的变化情况来决定买入或卖出股票。股民老张在研究股票的走势图时,发现一只股票的均线近期走得很有特点:如果按如图所示的方式建立平面直角坐标系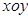 ,则股价
,则股价 (元)和时间
(元)和时间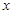 的关系在
的关系在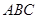 段可近似地用解析式
段可近似地用解析式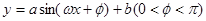 来描述,从
来描述,从 点走到今天的
点走到今天的 点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且
点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且 点和
点和 点正好关于直线
点正好关于直线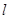 :
: 对称。老张预计这只股票未来的走势如图中虚线所示,这里
对称。老张预计这只股票未来的走势如图中虚线所示,这里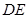 段与
段与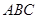 段关于直线
段关于直线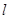 对称,
对称, 段是股价延续
段是股价延续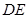 段的趋势(规律)走到这波上升行
段的趋势(规律)走到这波上升行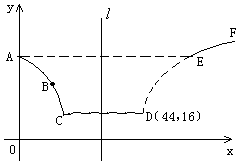
情的最高点 。现在老张决定取点
。现在老张决定取点
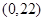 ,点
,点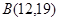 ,点
,点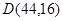 来确定解析式中的常数
来确定解析式中的常数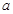 ,
,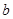 ,
, ,
,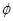 ,并且求得
,并且求得 。
。
(Ⅰ)请你帮老张算出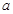 ,
,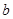 ,
,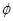 ,并回答股价什么时候见顶(即求
,并回答股价什么时候见顶(即求 点的横坐标)
点的横坐标)
(Ⅱ)老张如能在今天以 点处的价格买入该股票3000股,到见顶处
点处的价格买入该股票3000股,到见顶处 点的价格全部卖出,不计其它费用,这次操作他能赚多少元?
点的价格全部卖出,不计其它费用,这次操作他能赚多少元?
已知命题 :函数
:函数 在
在 上单调递增;命题
上单调递增;命题 :不等式
:不等式 的解集为
的解集为 ,若
,若 为真,
为真, 为假,求实数
为假,求实数 的取值范围.
的取值范围.
已知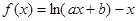 ,其中
,其中 ,
,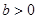 ,
,
(Ⅰ)若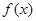 为
为 上的减函数,求
上的减函数,求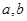 应满足的关系;
应满足的关系;
(Ⅱ)解不等式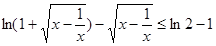 。
。