(10分)(1)已知
 且
且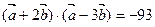 ,求向量
,求向量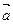 与
与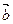 的夹角<
的夹角<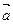 ,
,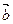 >;
>;
(2)设向量 ,
, ,
,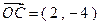 ,在向量
,在向量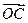 上是否存在点
上是否存在点 ,使得
,使得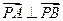 ,若存在,求出点
,若存在,求出点 的坐标;若不存在,请说明理由
的坐标;若不存在,请说明理由
..(本小题满分12分)如图,在正方体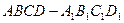 中,
中,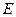 、
、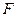 分别为棱
分别为棱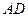 、
、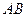 的中点.
的中点.
(1)求证: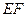 ∥平面
∥平面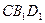 ;
;
(2)求证:平面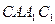 ⊥平面
⊥平面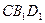 ;
;
(3)如果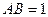 ,一个动点从点
,一个动点从点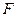 出发在正方体的
出发在正方体的
表面上依次经过棱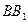 、
、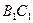 、
、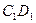 、
、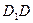 、
、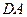 上的点,最终又回到点
上的点,最终又回到点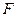 ,指出整个路线长度的最小值并说明理由.
,指出整个路线长度的最小值并说明理由.
.(本小题满分12分)已知函数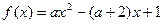 .若
.若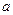 为整数,且函数
为整数,且函数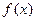 在
在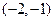 内恰有一个零点,求
内恰有一个零点,求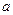 的值.
的值.
(本小题满分10分)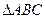 中,角A、B、C所对的边分别为
中,角A、B、C所对的边分别为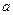 、
、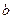 、
、 ,
,
已知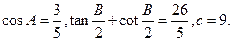
(1)求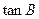 的值;(2)求
的值;(2)求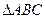 的面积。
的面积。
(
已知二次函数 满足条件
满足条件 且方程
且方程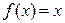 有等根
有等根
(1)求
(2)是否存在实数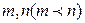 ,使得函数
,使得函数 在定义域为
在定义域为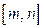 值域为
值域为 。如果存在,求出
。如果存在,求出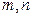 的值;如果不存在,说明理由
的值;如果不存在,说明理由
(.
已知函数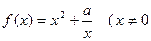 ,常数
,常数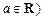 .
.
(1)讨论函数 的奇偶性,并说明理由;
的奇偶性,并说明理由;
( 2)若函数
2)若函数 在
在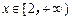 上为增函数,求
上为增函数,求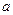 的取值范围.
的取值范围.