(12分)已知函数
(1)写出函数的单调递减区间;
(2)设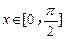 ,
,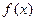 的最小值是
的最小值是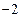 ,最大值是
,最大值是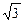 ,求实数
,求实数 的值
的值
已知数列 各项为非负实数,前n项和为
各项为非负实数,前n项和为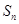 ,且
,且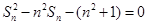
(1)求数列 的通项公式;
的通项公式;
(2)当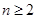 时,求
时,求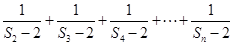 .
.
如图,从 到
到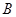 有6条网线,数字表示该网线单位时间内可以通过的最大信息量,现从中任取3条网线且使每条网线通过最大信息量,设这三条网线通过的最大信息之和为
有6条网线,数字表示该网线单位时间内可以通过的最大信息量,现从中任取3条网线且使每条网线通过最大信息量,设这三条网线通过的最大信息之和为 .
.
(1)当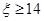 时,线路信息畅通,求线路信息畅通的概率;
时,线路信息畅通,求线路信息畅通的概率;
(2)求 的分布列和数学期望.
的分布列和数学期望.
已知函数 的最大值为2.
的最大值为2.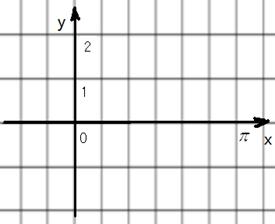
(1)求 的值及
的值及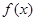 的最小正周期;
的最小正周期;
(2)在坐标纸上做出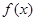 在
在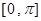 上的图像.
上的图像.
已知函数 .
.
(1)当 时,求函数
时,求函数 在
在 上的最大值;
上的最大值;
(2)令 ,若
,若 在区间
在区间 上不单调,求
上不单调,求 的取值范围;
的取值范围;
(3)当 时,函数
时,函数 的图象与
的图象与 轴交于两点
轴交于两点 ,且
,且 ,又
,又 是
是 的导函数.若正常数
的导函数.若正常数 满足条件
满足条件 ,证明:
,证明: .
.
已知等比数列 满足
满足 .
.
(1)求数列 的通项公式;
的通项公式;
(2)在 与
与 之间插入
之间插入 个数连同
个数连同 与
与 按原顺序组成一个公差为
按原顺序组成一个公差为 (
( )的等差数列.
)的等差数列.
①设 ,求数列
,求数列 的前
的前 和
和 ;
;
②在数列 中是否存在三项
中是否存在三项 (其中
(其中 成等差数列)成等比数列?若存在,求出这样的三项;若不存在,说明理由.
成等差数列)成等比数列?若存在,求出这样的三项;若不存在,说明理由.