(本小题满分12分)一商场对每天进店人数和商品销售件数进行了统计对比,得到如下表格:
人数 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
件数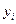 |
4 |
7 |
12 |
15 |
20 |
23 |
27 |
其中 .
.
(Ⅰ)以每天进店人数为横轴,每天商品销售件数为纵轴,画出散点图. (Ⅱ)求回归直线方程.(结果保留到小数点后两位)
(Ⅱ)求回归直线方程.(结果保留到小数点后两位)
(参考数据: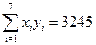 ,
, ,
, ,
, ,
,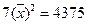 ,
, )
)
(Ⅲ)预测进店人数为80人时,商品销售的件数.(结果保留整数)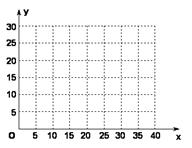
(本小题满分12分)
已知集合
(1)若 ;
;
(2)若 的充分条件,求实数
的充分条件,求实数 的取值范围。
的取值范围。
(本小题满分12分)
某同学参加3门课程的考试,假设该同学第一门课程取得优秀成绩的概率为 。第二、第三门课程取得优秀成绩的概率均为
。第二、第三门课程取得优秀成绩的概率均为 ,且不同课程是否取得优秀成绩相互独立。
,且不同课程是否取得优秀成绩相互独立。
(1)求该生恰有1门课程取得优秀成绩的概率;
(2)求该生取得优秀成绩的课程门数X的期望。
(本小题满分13分)
已知 (其中e为自然对数的底数)。
(其中e为自然对数的底数)。
(1)求函数
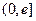 上的最小值;
上的最小值;
(2)是否存在实数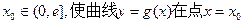 处的切线与y轴垂直?若存在,求出
处的切线与y轴垂直?若存在,求出 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
( 本小题满分12分)
本小题满分12分)
如图,ABCD是正方形空地,正方形的边长为30m,电源在点P处,点P到边AD、AB的距离分别为9m、3m。某广告公司计划在此空 地上竖一块长方形液
地上竖一块长方形液 晶广告屏幕MNEF,MN:NE=
晶广告屏幕MNEF,MN:NE= 16:9。线段MN必须过点P,满足M、N分别在边AD、AB上,设
16:9。线段MN必须过点P,满足M、N分别在边AD、AB上,设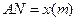 ,液晶广告屏幕MNEF的面积为
,液晶广告屏幕MNEF的面积为
(1)求S关于 的函数关系式,并与出该函数的定义域;
的函数关系式,并与出该函数的定义域;
(2)当 取何值时,液晶广告屏幕MNEF的面积S最小?
取何值时,液晶广告屏幕MNEF的面积S最小?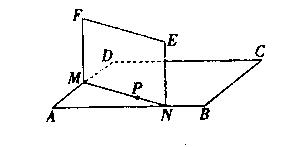
(本小题满分13分)
设函数 是定义域为R上的奇函数。
是定义域为R上的奇函数。
(1)若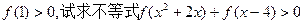 的解集;
的解集;
(2)若 上的最小值为—2,求m的值。
上的最小值为—2,求m的值。