(8分 )A、B两
)A、B两 地相距630千米,客车、货车分别从A、B两地同时出发,匀速相向行驶.货车两小时可到达途中C站,客车需9小时到达C站(如图1所示).货车的速度是客车的
地相距630千米,客车、货车分别从A、B两地同时出发,匀速相向行驶.货车两小时可到达途中C站,客车需9小时到达C站(如图1所示).货车的速度是客车的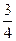 ,客、货车到C站的距离分别为y1、y2(千米),它们与行驶时间x(小
,客、货车到C站的距离分别为y1、y2(千米),它们与行驶时间x(小
时)之间的函数关系如图2所示.

(1)求客、货两车的速度;
(2)求两小时后,货车到C站的距离y2与行驶时间x之间的函数关系式;
(3)如图2,两函数图象交于点E,求E点坐标,并说明它所表示的实际意义.
(1)计算: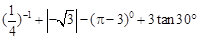
(2)解不等式组: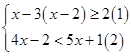
如图,抛物线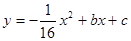 经过△ABC的三个顶点,点A坐标为(0,6),点C坐标为(4,6),点B在x轴正半轴上.
经过△ABC的三个顶点,点A坐标为(0,6),点C坐标为(4,6),点B在x轴正半轴上.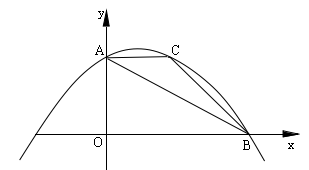
(1)求该抛物线的函数表达式和点B的坐标.
(2)将经过点B、C的直线平移后与抛物线交于点M,与x轴交于点N,当以B、C、M、N为顶点的四边形是平行四边形时,请求出点M的坐标.
(3)①动点D从点O开始沿线段OB向点B运动,同时以OD为边在第一象限作正方形ODEF,当正方形的顶点E恰好落在线段AB上时,则此时正方形的边长为.
②将①中的正方形ODEF沿OB向右平移,记平移中的正方形ODEF为正方形O′D′E′F′,当点D与点B重合时停止平移.设平移的距离为x,在平移过程中,设正方形O′D′E′F′与△ABC重叠部分的面积为y,请你画出相对应的图形并直接写出y与x之间的函数关系式.
某数学活动小组在一次活动中,对一个数学问题作如下探究:
【问题发现】如图1,在等边三角形ABC中,点M是边BC上任意一点,连接AM,以AM为边作等边三角形AMN,连接CN,证明:BM=CN.
【变式探究】如图2,在等腰三角形ABC中,BA=BC,∠ABC=∠α,点M为边BC上任意一点,以AM为腰作等腰三角形AMN,MA=MN,使∠AMN=∠ABC,连接CN,请求出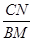 的值.
的值.
(用含α的式子表示出来)
【解决问题】如图3,在正方形ADBC中,点M为边BC上一点,以AM为边作正方形作AMEF,N为正方形AMEF的中心,连接CN,若正方形AMEF的边长为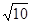 ,CN=
,CN= ,请你求正方形ADBC的边长.
,请你求正方形ADBC的边长.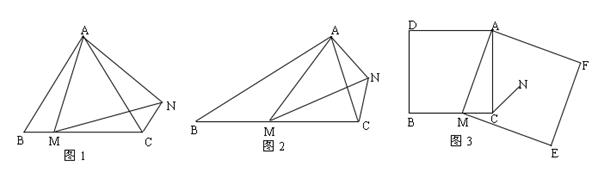
如图,AB是⊙O的直径,点E是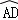 上的一点,∠DBC=∠BED.
上的一点,∠DBC=∠BED.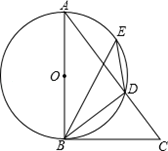
(1)请判断直线BC与⊙O的位置关系,并说明理由;
(2)已知AD=5,CD=4,求BC的长.
如图所示,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等.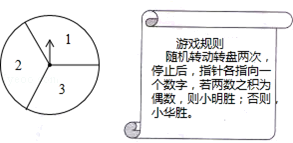
(1)现随机转动转盘一次,停止后,指针指向2的概率为;
(2)小明和小华利用这个转盘做游戏,若采用下列游戏规则,你认为对双方公平吗?请用列表或画树状图的方法说明理由.