(本小题满分14分)设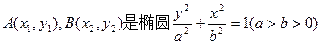
上的两点，已知向量
，
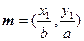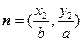,若
且椭圆的离心率
短轴长为2，
为坐标原点.
(Ⅰ)求椭圆的方程；
（Ⅱ）若直线
过椭圆的焦点
（0，c），（c为半焦距），求直线的斜率
的值；
（Ⅲ）试问：
的面积是否为定值？如果是，请给予证明；如果不是，请说明理由.
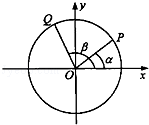
如图，以Ox为始边分别作角α与β（0＜α＜β＜π），它们的终边分别与单位圆相交于点P、Q，已知点P的坐标为（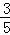
，
）．
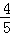（1）求sin2α的值；
（2）若β﹣α=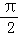
，求cos（α+β）的值．
如图，已知A、B是单位圆O上的点，C是圆与x轴正半轴的交点，点A的坐标为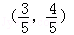
，点B在第二象限，且△AOB为正三角形．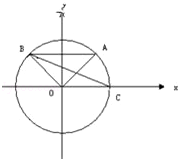
（Ⅰ）求sin∠COA；
（Ⅱ）求△BOC的面积．
已知点A（2，0），B（0，2），点C（x，y）在单位圆上．
（1）若|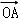
+
|=
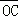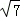（O为坐标原点），求
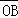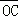与的夹角；
（2）若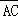
⊥
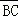，求点C的坐标．
已知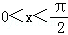
，用单位圆求证下面的不等式：
（1）sinx＜x＜tanx；
（2）
．
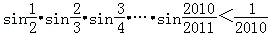如图，A、B是单位圆O上的点，C是圆O与x轴正半轴的交点，点A的坐标为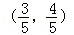
，三角形AOB为直角三角形．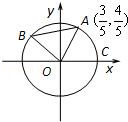
（1）求sin∠COA，cos∠COA的值；
（2）求cos∠COB的值．