已知椭圆C: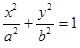
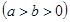 的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形.
的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形.
(1)求椭圆C的方程;
(2)过点Q(4,0)且不与坐标轴垂直的直线l交椭圆C于A、B两点,设点A关于x轴的
对称点为A1.求证:直线A1B过x轴上一定点,并求出此定点坐标.
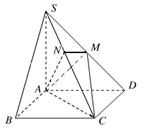
如图,在四棱锥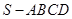 中,底面
中,底面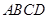 是正方形,
是正方形,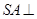 底面
底面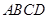 ,
,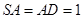 ,点
,点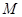 是
是 的中点,
的中点,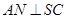 ,交
,交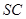 于点
于点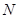 .
.
(1)求证:平面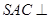 平面
平面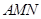 ;
;
(2)求三棱锥 的体积.
的体积.
城市公交车的数量若太多则容易造成资源的浪费;若太少又难以满足乘客需求.某市公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间作为样本分成5组,如下表所示(单位:分钟):
| 组别 |
候车时间 |
人数 |
| 一 |
 |
2 |
| 二 |
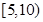 |
6 |
| 三 |
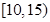 |
4 |
| 四 |
 |
2 |
| 五 |
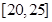 |
1 |
(1)估计这60名乘客中候车时间少于10分钟的人数;
(2)若从上表第三、四组的6人中任选2人作进一步的调查,求抽到的两人恰好来自不同组的概率.
如图所示,扇形AOB,圆心角AOB的大小等于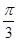 ,半径为2,在半径OA上有一动点C,过点C作平行于OB的直线交弧AB于点P.
,半径为2,在半径OA上有一动点C,过点C作平行于OB的直线交弧AB于点P.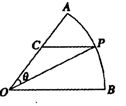
(1)若C是半径OA的中点,求线段PC的长;
(2)设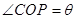 ,求
,求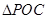 面积的最大值及此时
面积的最大值及此时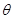 的值.
的值.
已知数列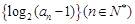 为等差数列,且
为等差数列,且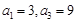 .
.
(1)求数列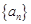 的通项公式;
的通项公式;
(2)证明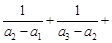 …
…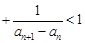 .
.