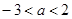(8分)已知以下基本事实:①对顶角相等;②一条直线截两条平行直线
所得的同位角相等;③两条直线 被第三条直线所截,若同位角相等,则这两条直线
被第三条直线所截,若同位角相等,则这两条直线
平行;④全等三角形的对应边、对应角分别相等.
(1)在利用以上基本事实作为依据来证明命题“两直线平行,内错角相等”时,必须要用的基本事实有 (填入序号即可);
(2)根据在(1)中的选择,结合所给图形,请你证明命题“两直线平行,内错角相等”.
已知:如图,_________________________________.
求证:_________________________________.
证明:
如图(1),△ABC与△EFD为等腰直角三角形,AC与DE重合,AB=AC=EF=3,∠BAC=∠DEF=90º,固定△ABC,将△DEF绕点A顺时针旋转,当DF边与AB边重合时,旋转中止.现不考虑旋转开始和结束时重合的情况,设DE,DF(或它们的延长线)分别交BC(或它的延长线) 于G,H点,如图(2)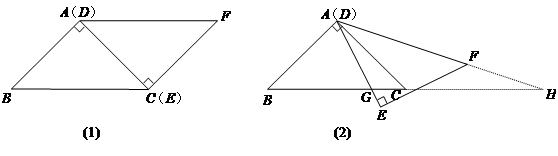
(1)问:始终与△AGC相似的三角形有 及 ;
(2)设CG=x,BH=y,求y关于x的函数关系式(只要求根据图(2)的情形说明理由);
(3)问:当x为何值时,△AGH是等腰三角形。
在“5.12大地震”灾民安置工作中,某企业接到一批生产甲种板材24000 和乙种板材12000
和乙种板材12000 的任务.(1)已知该企业安排140人生产这两种板材,每人每天能生产甲种板材30
的任务.(1)已知该企业安排140人生产这两种板材,每人每天能生产甲种板材30 或乙种板材20
或乙种板材20 .问:应分别安排多少人生产甲种板材和乙种板材,才能确保他们用相同的时间完成各自的生产任务?
.问:应分别安排多少人生产甲种板材和乙种板材,才能确保他们用相同的时间完成各自的生产任务?
(2)某灾民安置点计划用该企业生产的这批板材搭建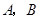 两种型号的板房共400间,在搭建过程中,按实际需要调运这两种板材.已知建一间
两种型号的板房共400间,在搭建过程中,按实际需要调运这两种板材.已知建一间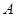 型板房和一间
型板房和一间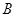 型板房所需板材及能安置的人数如下表所示:
型板房所需板材及能安置的人数如下表所示:
| 板房型号 |
甲种板材 |
乙种板材 |
安置人数 |
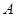 型板房 型板房 |
54  |
26  |
5 |
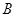 型板房 型板房 |
78  |
41  |
8 |
问:这400间板房最多能安置多少灾民?
如图,一次函数y=kx+b与反比例函数y=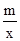 的图象交于A(4,6),B(-6,n)两点.(1)求一次函数与反比例函数的解析式;
的图象交于A(4,6),B(-6,n)两点.(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b<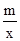 的解集______________;
的解集______________;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC. 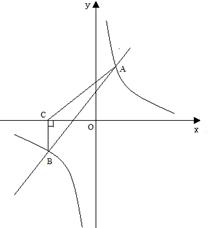
解方程: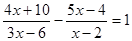
①化简: 
②先化简,再选择一个你喜欢的整数代入求值,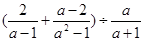 ,其中
,其中