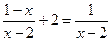在“5.12大地震”灾民安置工作中,某企业接到一批生产甲种板材24000 和乙种板材12000
和乙种板材12000 的任务.(1)已知该企业安排140人生产这两种板材,每人每天能生产甲种板材30
的任务.(1)已知该企业安排140人生产这两种板材,每人每天能生产甲种板材30 或乙种板材20
或乙种板材20 .问:应分别安排多少人生产甲种板材和乙种板材,才能确保他们用相同的时间完成各自的生产任务?
.问:应分别安排多少人生产甲种板材和乙种板材,才能确保他们用相同的时间完成各自的生产任务?
(2)某灾民安置点计划用该企业生产的这批板材搭建 两种型号的板房共400间,在搭建过程中,按实际需要调运这两种板材.已知建一间
两种型号的板房共400间,在搭建过程中,按实际需要调运这两种板材.已知建一间 型板房和一间
型板房和一间 型板房所需板材及能安置的人数如下表所示:
型板房所需板材及能安置的人数如下表所示:
| 板房型号 |
甲种板材 |
乙种板材 |
安置人数 |
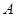 型板房 型板房 |
54  |
26  |
5 |
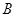 型板房 型板房 |
78  |
41  |
8 |
问:这400间板房最多能安置多少灾民?
欢欢有红色、白色、黄色三件上衣,又有米色、白色的两条裤子.
(1)她随机拿出一件上衣和一条裤子,用树状图(或列表法)表示所有可能出现的结果;
(2)如果欢欢最喜欢的穿着搭配是白色上衣配米色裤子,求欢欢随机拿出一件上衣和一条裤子正好是她最喜欢的穿着搭配的概率.
如图, F、C是线段AD上的两点,AB∥DE,BC∥EF ,AF=DC,
,AF=DC,
连结AE、BD,求证:四 边形ABDE是平行四边形。
边形ABDE是平行四边形。
如图2,正方形网格中,△ABC为格点三角形(顶点都是格
点),将△ABC绕点A按逆时针方向旋转90°得到 .
.
(1)在正方形网格中,作出 ;(不要求写作法)
;(不要求写作法)
(2)设网格小正方形的边长为1cm,求线段AB所扫过的图形的面积.(结果保留 )
)
先化简代数式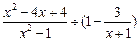 ,然后选取一个合适的x
,然后选取一个合适的x
代入求值.
解方程: