甲、乙两车同时从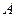 地出发,以各自的速度匀速向
地出发,以各自的速度匀速向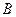 地行驶.甲车先到达
地行驶.甲车先到达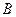 地,停留1小时后按原路以另一速度匀速返回,直到两车相遇.乙车的速度为每小时60千米.下图是两车之间的距离
地,停留1小时后按原路以另一速度匀速返回,直到两车相遇.乙车的速度为每小时60千米.下图是两车之间的距离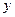 (千米)与乙车行驶时间
(千米)与乙车行驶时间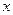 (小时)之间的
(小时)之间的 函数图象.
函数图象.
(1)两车行驶3小时后,两车相距 ▲ 千米;
(2)请在图中的( )内填上正确的值,并直接写出甲车从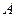 到
到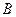 的行驶速度;
的行驶速度;
(3)求从甲车返回到与乙车相遇过程中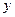 与
与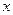 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量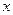 的取值
的取值
范围.
(4)求出甲车返回时的行驶速度及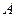 、
、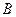 两地之间的距离.
两地之间的距离.
如图,矩形ABCD中,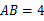 cm,
cm,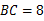 cm,动点M从点D出发,按折线DCBAD方向以2 cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1 cm/s的速度运动.
cm,动点M从点D出发,按折线DCBAD方向以2 cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1 cm/s的速度运动.
(1)若动点M、N同时出发,经过几秒钟两点相遇?
(2)若点E在线段BC上,且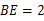 cm,若动点M、N同时出发,相遇时停止运动,经过几秒钟,点A、E、M、N组成平行四边形?
cm,若动点M、N同时出发,相遇时停止运动,经过几秒钟,点A、E、M、N组成平行四边形?
如图,四边形ABCD是菱形,CE⊥AB交AB的延长线于点E,CF⊥AD交AD的延长线于点F,请猜想,CE和CF的大小有什么关系?并证明你的猜想.
商场销售某种产品,一月份销售了若干件,共获利润30 000元.二月份将这种商品的单价降低了0.4元.但销售量比一月份增加了5 000件,从而获得利润比一月份多2 000元. 求调价前每件商品的利润是多少元?
如图,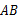 是⊙
是⊙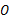 的直径,
的直径,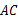 是⊙
是⊙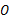 的弦,以
的弦,以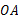 为直径的⊙
为直径的⊙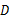 与
与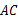 相交于点
相交于点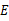 ,
,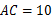 ,求
,求 的长.
的长.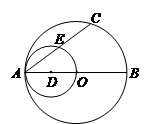
如图, 、
、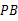 是⊙O的两条切线,
是⊙O的两条切线,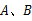 是切点,
是切点, 是⊙
是⊙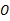 的直径,若∠
的直径,若∠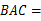 40°,求∠
40°,求∠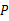 的度数.
的度数.