如图,矩形ABCD中,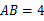 cm,
cm,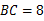 cm,动点M从点D出发,按折线DCBAD方向以2 cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1 cm/s的速度运动.
cm,动点M从点D出发,按折线DCBAD方向以2 cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1 cm/s的速度运动.
(1)若动点M、N同时出发,经过几秒钟两点相遇?
(2)若点E在线段BC上,且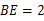 cm,若动点M、N同时出发,相遇时停止运动,经过几秒钟,点A、E、M、N组成平行四边形?
cm,若动点M、N同时出发,相遇时停止运动,经过几秒钟,点A、E、M、N组成平行四边形?
已知二次函数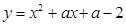
(1)求证:不论a为何实数,此函数图象与x轴总有两个交点.
(2)设a<0,当此函数图象与x轴的两个交点的距离为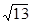 时,求出此二次函数的解析式.
时,求出此二次函数的解析式.
(3)在(2)的条件下,若此二次函数图象与x轴交于A、B两点,在函数图象上是否存在点P,使得△PAB的面积为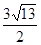 ,若存在求出P点坐标,若不存在请说明理由。
,若存在求出P点坐标,若不存在请说明理由。
当抛物线的解析式中含有字母系数时,随着系数中的字母取值的不同,抛物线的顶点坐标也将发生变化.例如:由抛物线y=x2-2mx+m2+2m-1①有y=(x-m)2+2m-1②,
所以抛物线顶点坐标为(m,2m-1),即x=m③,y=2m-1④.
当m的值变化时,x,y的值也随之变化,因而y的值也随x值的变化而变化.
将③代入④,得y=2x-1⑤.可见,不论m取任何实数,抛物线顶点的纵坐标y和横坐标x都满足关系式:y=2x-1;
根据上述阅读材料提供的方法,确定点(-2m, m-1)满足的函数关系式为_______.
(2)根据阅读材料提供的方法,确定抛物线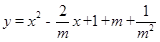 顶点的纵坐标y与横坐标x之间的关系式.
顶点的纵坐标y与横坐标x之间的关系式.
某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元).
设每件商品的售价上涨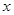 元(
元(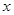 为正整数),每个月的销售利润为
为正整数),每个月的销售利润为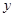 元.
元.
(1)求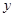 与
与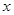 的函数关系式并直接写出自变量
的函数关系式并直接写出自变量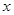 的取值范围;
的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3)每件商品的售价定为多少元时,每个月的利润恰为2200元?根据以上结论,请你直接写出售价在什么范围时,每个月的利润不低于2200元?
如图,直线y=3x和y=2x分别与直线x=2相交于点A、B,将抛物线y=x2沿线段OB移动,使其顶点始终在线段OB上,抛物线与直线x=2相交于点C,设△AOC的面积为S,求S的取值范围.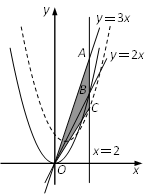
如图,直角△ABC中,∠C=90°,AB=2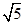 ,sinB=
,sinB=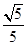 ,点P为边BC上一动点,PD∥AB,PD交AC于点D,连结AP.
,点P为边BC上一动点,PD∥AB,PD交AC于点D,连结AP.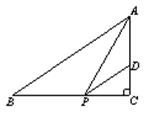
(1)求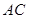 、
、 的长;
的长;
(2)设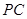 的长为
的长为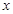 ,
, 的面积为
的面积为 .当
.当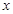 为何值时,
为何值时, 最大并求出最大值.
最大并求出最大值.