已知等差数列 满足:
满足: ,
,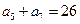 ,
, 的前n项和为
的前n项和为 .
.
(Ⅰ)求 及
及 ;
;
(Ⅱ)令bn=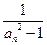 (
(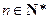 ),求数列
),求数列 的前n项和
的前n项和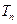 .
.
锐角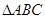 中,角
中,角 的对边分别是
的对边分别是 ,已知
,已知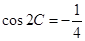 ,
,
(1)求 的值;
的值;
(2)当 时,求
时,求 的长及
的长及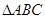 的面积.
的面积.
(1)已知 ,若关于
,若关于 不等式的解集为空集,求
不等式的解集为空集,求 的取值范围;
的取值范围;
(2) 已知 ,且
,且 ,求证:
,求证:
在直角坐标系 中,直线
中,直线 的参数方程为
的参数方程为 为参数),若以O点为极点,
为参数),若以O点为极点, 轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为
轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为 。
。
(1)求曲线C的直角坐标方程及直线 的普通方程;
的普通方程;
(2)将曲线C上各点的横坐标缩短为原来的 ,再将所得曲线向左平移1个单位,得到曲线
,再将所得曲线向左平移1个单位,得到曲线 ,求曲线
,求曲线 上的点到直线
上的点到直线 的距离的最小值
的距离的最小值
如图,AB是圆O的直径,弦BD、CA的延长线相交于点E,EF垂直BA的延长线于点F.
求证:(1) ;
;
(2)AB2=BE•BD-AE•AC.
已知函数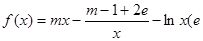 为自然对数的底数),
为自然对数的底数),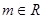 。
。
(1)当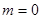 时,求函数
时,求函数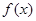 的单调区间和极值;
的单调区间和极值;
(2)已知函数 在
在 上为增函数,且
上为增函数,且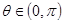 ,若在
,若在 上至少存在一个实数
上至少存在一个实数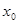 ,使得
,使得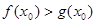 成立,求
成立,求 的取值范围。
的取值范围。