(本小题14分)已知f(x)=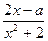 (x∈R)在区间[-1,1]上是增函数,
(x∈R)在区间[-1,1]上是增函数,
(1)求实数a的值组成的集合A;
(2)设关于x的方程f(x)= 的两个非零实根为x1、x2。试问:是否存在实数m,使得不等
的两个非零实根为x1、x2。试问:是否存在实数m,使得不等
式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
如图所示,已知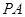 与⊙
与⊙ 相切,
相切,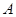 为切点,
为切点, 为割线,弦
为割线,弦 ,
, 相交于
相交于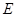 点,
点, 为
为 上一点,且
上一点,且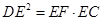 .
.
(1)求证: ;
;
(2)求证: .
.
已知函数
(1)若 且函数
且函数 在区间
在区间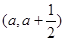 上存在极值,求实数
上存在极值,求实数 的取值范围;
的取值范围;
(2)如果当 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数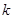 的取值范围.
的取值范围.
如图,已知点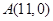 ,函数
,函数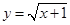 的图象上的动点
的图象上的动点 在
在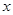 轴上的射影为
轴上的射影为 ,且点
,且点 在点
在点 的左侧.设
的左侧.设 ,
, 的面积为
的面积为 .
.
(Ⅰ)求函数 的解析式及
的解析式及 的取值范围;
的取值范围;
(Ⅱ)求函数 的最大值.
的最大值.
如图,斜三棱柱ABC-A'B'C'中,底面是边长为a的正三角形,侧棱长为b,侧棱AA'与底面相邻两边AB,AC都成45°角.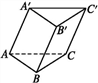
(Ⅰ)求此斜三棱柱的表面积.
(Ⅱ)求三棱锥B'-ABC的体积.
设函数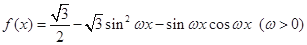 ,且
,且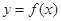 的图象的一个对称中心到最近的对称轴的距离为
的图象的一个对称中心到最近的对称轴的距离为 ,
,
(Ⅰ)求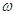 的值
的值
(Ⅱ)求 在区间
在区间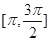 上的最大值和最小值.
上的最大值和最小值.