如图所示,直空中有以O′为圆心,r为半径的圆柱形匀强磁场区域,圆的最下端与 x轴相切于直角坐标原点O,圆的右端与平行于y轴的虚线MN相切,磁感应强度为B,方向垂直纸面向外,在虚线MN右侧x轴上方足够大的范围内有方向竖直向下、场强大小为E的匀强电场。现从坐标原点O向纸面不同方向发射速率相同的质子,质子在磁场中做匀速圆周运动的半径也为r,已知质子的电荷量为e,质量为m,不计质子的重力、质子对电
x轴相切于直角坐标原点O,圆的右端与平行于y轴的虚线MN相切,磁感应强度为B,方向垂直纸面向外,在虚线MN右侧x轴上方足够大的范围内有方向竖直向下、场强大小为E的匀强电场。现从坐标原点O向纸面不同方向发射速率相同的质子,质子在磁场中做匀速圆周运动的半径也为r,已知质子的电荷量为e,质量为m,不计质子的重力、质子对电 磁场的影响及质子间的相互作用力。求:
磁场的影响及质子间的相互作用力。求:
(1)质子进入磁场时的速度 大小
大小
(2)沿y轴正方向射入磁场的质子到达x轴所需的时间。
如图,虚线框内为某种电磁缓冲车的结构示意图,其主要部件为缓冲滑块 和质量为
和质量为 的缓冲车厢.在缓冲车的底板上,沿车的轴线固定着两个光滑水平绝缘导轨PQ、MN.缓冲车的底部,安装电磁铁(图中未画出),能产生垂直于导轨平面的匀强磁场,磁场的磁感应强度为B.导轨内的缓冲滑块
的缓冲车厢.在缓冲车的底板上,沿车的轴线固定着两个光滑水平绝缘导轨PQ、MN.缓冲车的底部,安装电磁铁(图中未画出),能产生垂直于导轨平面的匀强磁场,磁场的磁感应强度为B.导轨内的缓冲滑块 由高强度绝缘材料制成,滑块
由高强度绝缘材料制成,滑块 上绕有闭合矩形线圈
上绕有闭合矩形线圈 ,线圈的总电阻为
,线圈的总电阻为 ,匝数为
,匝数为 ,
, 边长为
边长为 .假设缓冲车以速度
.假设缓冲车以速度 与障碍物
与障碍物 碰撞后,滑块
碰撞后,滑块 立即停下,此后线圈与轨道的磁场作用力使缓冲车厢减速运动,从而实现缓冲,一切摩擦阻力不计.
立即停下,此后线圈与轨道的磁场作用力使缓冲车厢减速运动,从而实现缓冲,一切摩擦阻力不计.
(1)求滑块 的线圈中最大感应电动势的大小;
的线圈中最大感应电动势的大小;
(2)若缓冲车厢向前移动距离 后速度为零,缓冲车厢与障碍物和线圈的
后速度为零,缓冲车厢与障碍物和线圈的 边均没有接触,则此过程线圈
边均没有接触,则此过程线圈 中通过的电量和产生的焦耳热各是多少?
中通过的电量和产生的焦耳热各是多少?
如图,喷雾器内有一定体积的水,初始时上部封闭有压强为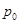 、体积为
、体积为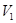 的空气.关闭喷雾阀门,用打气筒向喷雾器内再充入压强为
的空气.关闭喷雾阀门,用打气筒向喷雾器内再充入压强为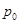 、体积为
、体积为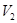 的空气(设外界环境温度一定,空气可看作理想气体).
的空气(设外界环境温度一定,空气可看作理想气体).
①当水面上方被封气体温度与外界温度相等时,求气体压强.
②打开喷雾阀门,喷雾过程中封闭气体可以看成等温膨胀,此过程气体是“吸热”、“放热”或“既不吸热也不放热”?
平时擦玻璃时,我们经常会用到如图甲所示的“魔力刷”.使用时,两个一样的刷子分别位于玻璃窗户玻璃板的两侧,两刷子靠磁铁的吸引力吸在玻璃上,当移动其中一块刷子时,另一块刷子会跟到移动,达到同时清洁玻璃内外侧的目的.已知:某种品牌玻璃刷的每个刷子的质量都为 ,与玻璃的滑动摩擦因数均为
,与玻璃的滑动摩擦因数均为 ,且最大静摩擦力等于滑动摩擦力,重力加速度取
,且最大静摩擦力等于滑动摩擦力,重力加速度取 .
.
(1)将其中一个刷子用与竖直方向成 的推力压在竖直玻璃上,如题9图乙所示,现要把刷子沿竖直方向向上推动,求推力的最小值
的推力压在竖直玻璃上,如题9图乙所示,现要把刷子沿竖直方向向上推动,求推力的最小值
(2)把两个刷子对齐分别放在竖直玻璃板的两侧,如题9图丙所示,现用与竖直方向成 ,大小为
,大小为 的拉力向下拉动内侧的刷子时,外侧刷子将立即跟着移动且很快与内侧刷子保持相对静止.此时刷子磁铁间的吸引力在垂直玻璃板面方向的分量恒为
的拉力向下拉动内侧的刷子时,外侧刷子将立即跟着移动且很快与内侧刷子保持相对静止.此时刷子磁铁间的吸引力在垂直玻璃板面方向的分量恒为 ,求刷子间的磁铁吸引力在沿玻璃板面切线方向的分量.
,求刷子间的磁铁吸引力在沿玻璃板面切线方向的分量.
(3)假设玻璃是边长为 的正方形,刷子是边长为
的正方形,刷子是边长为 的正方形;当两刷子的正对面积大于一半时,刷子磁铁间的吸引力的垂直分量和切向分量均不变,当两刷子的正对面积小于或等于一半时,两刷子就无法吸引在一起.在(2)的情况下,若拉力方向不变,大小变为
的正方形;当两刷子的正对面积大于一半时,刷子磁铁间的吸引力的垂直分量和切向分量均不变,当两刷子的正对面积小于或等于一半时,两刷子就无法吸引在一起.在(2)的情况下,若拉力方向不变,大小变为 ,要使一次性向下拉动刷子就可以完成清理玻璃的竖边,求
,要使一次性向下拉动刷子就可以完成清理玻璃的竖边,求 的取值范围.
的取值范围.
 如图所示,纸面内有一固定的金属导轨,它由长为
如图所示,纸面内有一固定的金属导轨,它由长为 的直线段
的直线段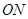 和以
和以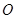 点为圆心、半径为
点为圆心、半径为 、在
、在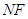 处开有小缺口的圆环两部分组成. 另一直导线
处开有小缺口的圆环两部分组成. 另一直导线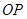 以
以 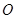 为圆心,沿逆时针方向匀速转动,周期为
为圆心,沿逆时针方向匀速转动,周期为 .直导线
.直导线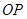 与导轨接触良好,导轨和直导线单位长度电阻均为
与导轨接触良好,导轨和直导线单位长度电阻均为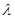 .整个空间有磁感应强度为
.整个空间有磁感应强度为 、方向垂直于纸面向外的匀强磁场.当直导线
、方向垂直于纸面向外的匀强磁场.当直导线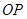 转动到与
转动到与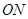 的夹角为
的夹角为 (只考虑
(只考虑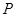 到达
到达 点之前的情况)时,求
点之前的情况)时,求 
(1)固定导轨消耗的电功率;
(2)圆环缺口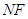 两端的电势差
两端的电势差 .
.
如图所示的钢板由倾斜部分和水平部分组成,水平部分足够长,两部分之间由一小段圆弧面相连接.在钢板的中间有位于竖直面内的光滑圆槽轨道,斜面的倾角为 .现有两个质量均为
.现有两个质量均为 、半径均为
、半径均为 (不能忽略)的均匀球沿圆槽轨道排列,在施加于1号球的水平外力作用下均静止,此时1号球球心距它在水平槽运动时的球心高度差为
(不能忽略)的均匀球沿圆槽轨道排列,在施加于1号球的水平外力作用下均静止,此时1号球球心距它在水平槽运动时的球心高度差为 .现撤去外力使小球开始滑动,然后两个小球均以相同速度滑动到水平槽内.已知整个过程中系统无机械能损失,重力加速度为
.现撤去外力使小球开始滑动,然后两个小球均以相同速度滑动到水平槽内.已知整个过程中系统无机械能损失,重力加速度为 .求:
.求:
(1)两球在水平槽中一起匀速运动的速度.
(2)从开始运动到两球在水平槽中一起匀速运动的过程中,1号球机械能的变化量