(本小题满分12分)一个口袋内装有形状、大小相同的2个白球和3个黑球。
(1)从中随机地摸出一个球不放回,再随机地摸出一个球,求两球同时是黑球的概率;
(2)从中随机地摸出一个球,放回后再随机地摸出一个球,求两球颜色恰好不同的概率
已知函数 (其中
(其中 >0,
>0, )的最小正周期为
)的最小正周期为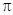 .
.
(1)求 的值;
的值;
(2)在△ 中,若
中,若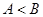 ,且
,且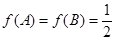 ,求
,求 .
.
对于函数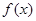 ,若存在
,若存在 ,使得
,使得 成立,则称
成立,则称 为
为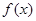 的天宫一号点.已知函数
的天宫一号点.已知函数 的两个天宫一号点分别是
的两个天宫一号点分别是 和2 .
和2 .
(1)求 的值及
的值及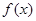 的表达式;
的表达式;
(2)试求函数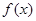 在区间
在区间 上的最大值
上的最大值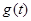 .
.
两个重要城市之间人员交流频繁,为了缓解交通压力,特修一条专用铁路,用一列火车作为交通车. 已知该车每次拖4节车厢,一日能来回16次, 如果每次拖7节车厢,则每日能来回10次.
(1)若每日来回的次数是车头每次拖挂车厢节数的一次函数,求此一次函数解析式;
(2)在(1)的条件下,每节车厢能载乘客110人.问这列火车每天来回多少次才能使运营人数最多?并求出每天最多运营人数
函数 .
.
(1) 讨论 的奇偶性;
的奇偶性;
(2) 若函数 的图象经过点(2,
的图象经过点(2, ), 求
), 求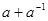 的值.
的值.
已知函数
(1) 求证: 在
在 上是增函数;
上是增函数;
(2) 若 在区间
在区间 上取得最大值为5,求实数
上取得最大值为5,求实数 的值.
的值.