对于函数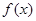 ,若存在
,若存在 ,使得
,使得 成立,则称
成立,则称 为
为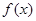 的天宫一号点.已知函数
的天宫一号点.已知函数 的两个天宫一号点分别是
的两个天宫一号点分别是 和2 .
和2 .
(1)求 的值及
的值及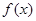 的表达式;
的表达式;
(2)试求函数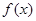 在区间
在区间 上的最大值
上的最大值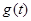 .
.
(本小题满分12分)如图,圆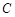 与
与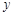 轴相切于点
轴相切于点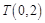 ,与
,与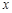 轴正半轴相交于两点
轴正半轴相交于两点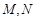 (点
(点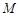 在点
在点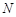 的左侧),且
的左侧),且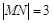 .
.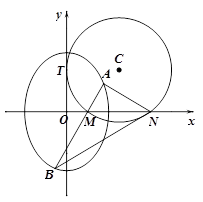
(Ⅰ)求圆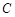 的方程;
的方程;
(Ⅱ)过点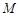 任作一条直线与椭圆
任作一条直线与椭圆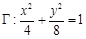 相交于两点
相交于两点 ,连接
,连接 ,求证:
,求证: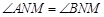 .
.
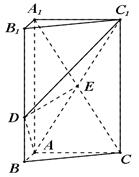
(本小题满分12分)如图,三棱柱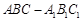 中,
中,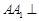 平面
平面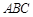 ,
,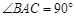 ,
,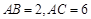 , 点
, 点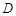 在线段
在线段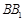 上,且
上,且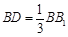 ,
,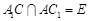 .
.
(Ⅰ)求证:直线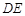 与平面
与平面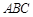 不平行;
不平行;
(Ⅱ)设平面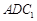 与平面
与平面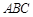 所成的锐二面角为
所成的锐二面角为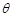 ,若
,若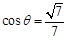 ,求
,求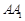 的长;
的长;
(Ⅲ)在(Ⅱ)的条件下,设平面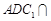 平面
平面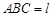 ,求直线
,求直线 与
与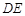 所成的角的余弦值.
所成的角的余弦值.
(本小题满分12分)西安市某中学在每年的11月份都会举行“文化艺术节”,开幕式当天组织举行大型的文艺表演,同时邀请36名不同社团的社长进行才艺展示.其中有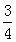 的社长是高中学生,
的社长是高中学生,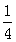 的社长是初中学生,高中社长中有
的社长是初中学生,高中社长中有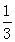 是高一学生,初中社长中有
是高一学生,初中社长中有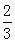 是初二学生.
是初二学生.
(Ⅰ)若校园电视台记者随机采访3位社长,求恰有1人是高一学生且至少有1人是初中学生的概率;
(Ⅱ)若校园电视台记者随机采访3位初中学生社长,设初二学生人数为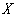 ,求
,求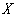 的分布列及数学期望
的分布列及数学期望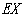 .
.
(本小题满分12分)已知等差数列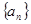 满足:
满足: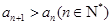 ,
,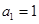 ,该数列的前三项分别加上1,1,3后成等比数列,
,该数列的前三项分别加上1,1,3后成等比数列,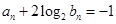 .
.
(Ⅰ)分别求数列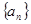 ,
,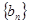 的通项公式;
的通项公式;
(Ⅱ)求证:数列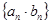 的前
的前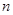 项和
项和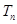
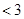 .
.
(本小题满分10分)已知数列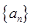 通项公式为
通项公式为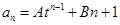 ,其中
,其中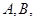
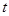 为常数,且
为常数,且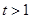 ,
,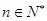 .等式
.等式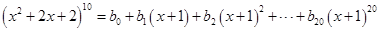 ,其中
,其中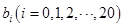 为实常数.
为实常数.
(1)若 ,求
,求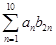 的值;
的值;
(2)若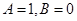 ,且
,且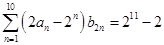 ,求实数
,求实数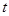 的值.
的值.