(理)在长方体ABCD—A1B1C1D1,中,AD=AA1=1,AB=2,点E在棱
AD上移动.
(1)证明:D1E⊥A1D;
(2)当E为AB的中点时,求点E到面ACD1的距离;
(3)AE等于何值时,二面角D1—EC—D的大小为 。
。
已知向量 且A、B、C分别为△ABC的三边a、b、c所对的角
且A、B、C分别为△ABC的三边a、b、c所对的角
(1)求角C的大小;(2)若 ,求c边的长。
,求c边的长。
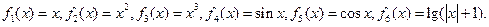 分别写在六张卡片上,放在一盒子中。 (1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数卡片则停止抽取,否则继续进行,求抽取次数
分别写在六张卡片上,放在一盒子中。 (1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数卡片则停止抽取,否则继续进行,求抽取次数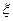 的分布列和数学期望.
的分布列和数学期望.
已知函数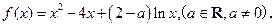
(1)当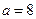 时,求函数
时,求函数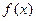 的单调区间;
的单调区间;
(2)求函数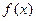 在区间
在区间 上的最小值.
上的最小值.
已知椭圆 的中心在原点,焦点在
的中心在原点,焦点在 轴上,椭圆上的点到焦点的距离的最小值为
轴上,椭圆上的点到焦点的距离的最小值为 ,离心率为
,离心率为 .
.
(1)求椭圆 的方程;
的方程;
(2)过点 作直线
作直线 交
交 于
于 、
、 两点,试问:在
两点,试问:在 轴上是否存在一个定点
轴上是否存在一个定点 ,使
,使 为定值?若存在,求出这个定点
为定值?若存在,求出这个定点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
已知直角梯形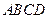 中,
中, ,
,
 过
过 作
作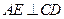 ,垂足为
,垂足为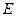 ,
,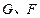 分别为
分别为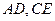 的中点,现将
的中点,现将 沿
沿 折叠使二面角
折叠使二面角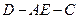 的平面角的正切值为
的平面角的正切值为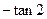 .
.
(1)求证: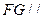 平面
平面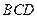 ;
;
(2)求异面直线 与
与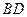 所成的角的余弦值;
所成的角的余弦值;
(3)求二面角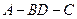 的大小.
的大小.