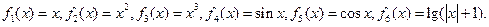 分别写在六张卡片上,放在一盒子中。 (1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数卡片则停止抽取,否则继续进行,求抽取次数
分别写在六张卡片上,放在一盒子中。 (1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数卡片则停止抽取,否则继续进行,求抽取次数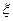 的分布列和数学期望.
的分布列和数学期望.
公安部发布酒后驾驶处罚的新规定(一次性扣罚12分)已于2011年4月1日起正式施行.酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量 (简称血酒含量,单位是毫克/100毫升),当
(简称血酒含量,单位是毫克/100毫升),当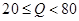 时,为酒后驾车;当
时,为酒后驾车;当 时,为醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量(如下表).
时,为醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量(如下表).
| 血酒含量 |
(0,20) |
[20,40) |
[40,60) |
[60,80) |
[80,100) |
[100,120] |
| 人数 |
194 |
1 |
2 |
1 |
1 |
1 |
依据上述材料回答下列问题:
(Ⅰ)分别写出酒后违法驾车发生的频率和酒后违法驾车中醉酒驾车的频率;
(Ⅱ)从酒后违法驾车的司机中,抽取2人,请一一列举出所有的抽取结果,并求取到的2人中含有醉酒驾车的概率. (酒后驾车的人用大写字母如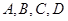 表示,醉酒驾车的人用小写字母如
表示,醉酒驾车的人用小写字母如 表示)
表示)
如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且2PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.
(Ⅰ)求异面直线EF与AG所成角的余弦值;
(Ⅱ)求证:BC∥面EFG;
(Ⅲ)求三棱锥E-AFG的体积.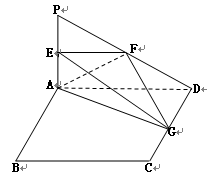
在等差数列 中,
中, ,其前
,其前 项和为
项和为 ,等比数列
,等比数列 的各项均为正数,
的各项均为正数, ,公比为
,公比为 ,且
,且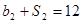 ,
,  .
.
(Ⅰ)求 与
与 ;(Ⅱ)设数列
;(Ⅱ)设数列 满足
满足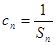 ,求
,求 的前
的前 项和
项和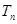
已知函数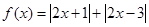
(Ⅰ)求不等式 ≤6的解集;
≤6的解集;
(Ⅱ)若关于x的不等式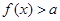 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
以直角坐标系的原点为极点,x轴的正半轴为极轴,建立极坐标系,并在两种坐标系中取相同的单位长度.已知直线l的极坐标方程为 ,曲线C的参数方程为
,曲线C的参数方程为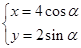 (α为参数).
(α为参数).
(Ⅰ)求直线l的直角坐标方程和曲线C的普通方程;
(Ⅱ)若直线l与曲线C交于A、B两点,求线段AB的长