已知直角梯形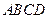 中,
中, ,
,
 过
过 作
作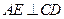 ,垂足为
,垂足为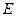 ,
,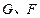 分别为
分别为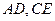 的中点,现将
的中点,现将 沿
沿 折叠使二面角
折叠使二面角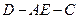 的平面角的正切值为
的平面角的正切值为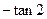 .
.
(1)求证: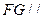 平面
平面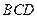 ;
;
(2)求异面直线 与
与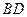 所成的角的余弦值;
所成的角的余弦值;
(3)求二面角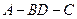 的大小.
的大小.
△ABC的三个内角为A,B,C,当A为时,cosA+2cos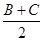 取得最大值,
取得最大值,
且这个最大值为.
已知 =
=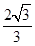 ,那么sin
,那么sin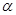 的值为 ,cos2
的值为 ,cos2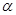 的值为
的值为
(本小题满分15分)
已知椭圆C:+=1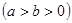 的离心率为,左焦点为F(-1,0),
的离心率为,左焦点为F(-1,0),
(1) 设A,B分别为椭圆的左、右顶点,过点F且斜率为k的直线L与椭圆C交于M,N两点,若 ,求直线L的方程;
,求直线L的方程;
(2)椭圆C上是否存在三点P,E,G,使得S△OPE=S△OPG=S△OEG=?
(本小题满分15分)已知函数
(Ⅰ)若曲线 在点
在点 处的切线与直线
处的切线与直线 平行,求
平行,求 的值;
的值;
(Ⅱ)记 ,
, ,且
,且 .求函数
.求函数 的单调递增区间.
的单调递增区间.
(本小题满分14分)已知四棱锥P—GBCD中(如图),PG⊥平面GBCD,GD∥BC,GD= BC,且BG⊥GC,GB=GC=2,E是BC的中点,PG=4
BC,且BG⊥GC,GB=GC=2,E是BC的中点,PG=4
(Ⅰ)求异面直线GE与PC所成角的余弦值;
(Ⅱ)若F点是棱PC上一点,且 ,
, ,求
,求 的值.
的值.