已知圆 的半径为
的半径为 ,圆心
,圆心 在直线
在直线 上.
上.
(Ⅰ)若圆 被直线
被直线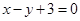 截得的弦长为
截得的弦长为 ,求圆
,求圆 的标准方程;
的标准方程;
(Ⅱ)设点 ,若圆
,若圆 上总存在两个点到点
上总存在两个点到点 的距离为
的距离为 ,求圆心
,求圆心 的横坐标
的横坐标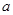 的取值范围.
的取值范围.
(每小题6分,共12分)(1)函数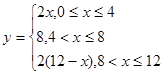 ,编写出求函数的函数值的程序(使用嵌套式);
,编写出求函数的函数值的程序(使用嵌套式);
(2)“求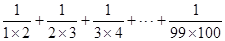 的值.”写出用基本语句编写的程序(使用当型).
的值.”写出用基本语句编写的程序(使用当型).
(本小题满分14分)已知函数 ..
..
(Ⅰ)若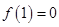 ,求函数
,求函数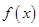 的最大值;
的最大值;
(Ⅱ)令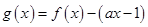 ,求函数
,求函数 的单调区间;
的单调区间;
(Ⅲ)若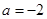 ,正实数
,正实数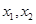 满足
满足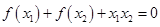 ,证明
,证明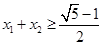 .
.
(本小题满分13分)已知以C为圆心的动圆过定点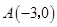 ,且与圆
,且与圆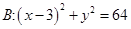 (B为圆心)相切,点C的轨迹为曲线T.设Q为曲线T上(不在x轴上)的动点,过点A作OQ(O为坐标原点)的平行线交曲线T于M,N两点.
(B为圆心)相切,点C的轨迹为曲线T.设Q为曲线T上(不在x轴上)的动点,过点A作OQ(O为坐标原点)的平行线交曲线T于M,N两点.
(Ⅰ)求曲线T的方程;
(Ⅱ)是否存在常数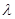 ,使
,使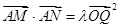 总成立?若存在,求
总成立?若存在,求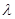 ;若不存在,说明理由.
;若不存在,说明理由.
(本小题满分12分)已知数列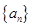 的前
的前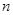 项和为
项和为 .
.
(Ⅰ)求数列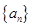 的通项公式;
的通项公式;
(Ⅱ)设集合 ,等差数列
,等差数列 的任一项
的任一项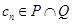 ,其中
,其中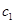 是
是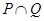 中的最小数,
中的最小数,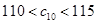 ,求数列
,求数列 的通项公式.
的通项公式.
(本小题满分12分)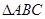 是边长为4的等边三角形,
是边长为4的等边三角形, 是等腰直角三角形,
是等腰直角三角形,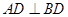 ,平面
,平面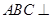 平面ABD,且
平面ABD,且 平面ABC,EC=2.
平面ABC,EC=2.
(Ⅰ)证明:DE//平面ABC;
(Ⅱ)证明: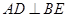 .
.