2011年夏季，河南小麦喜获丰收，现有甲种小麦1530吨，乙种小麦1150
吨，需安排A、B两种不同规格的货厢50节把小麦全部运往上海.已知用一节A型货厢的运
费是0.5万元，用一节B型货厢的运费是0.8万元.
（1）设运输这批小麦的总运费为y (万元)，用A型货箱的节数为x (节)，试写出y与x
之间的函数关系式；
（2）已知甲种小麦35吨和乙种小麦15吨，可装满一节A型货厢；甲种小麦25吨和乙种小麦35吨可装满一节B型货厢，按此要求安排A、B两种货厢的节数，有哪几种运输方案？请你设计出来.
（3）利用函数的性质说明，在这些方案中，哪种方案总运费最少？最少运费是多少万元？
如图，抛物线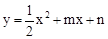
与x轴交于A、B两点，与y轴交于C点，四边形OBHC为矩形，CH的延长线交抛物线于点D（5，2），连结BC、AD.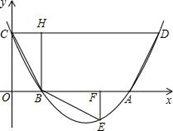
（1）求C点的坐标及抛物线的解析式；
（2）将△BCH绕点B按顺时针旋转90°后再沿x轴对折得到△BEF（点C与点E对应），判断点E是否落在抛物线上，并说明理由；
（3）设过点E的直线交AB边于点P，交CD边于点Q.问是否存在点P，使直线PQ分梯形ABCD的面积为1∶3两部分？若存在，求出P点坐标；若不存在，请说明理由.
如图，一次函数y=kx+n的图象与x轴和y轴分别交于点A（6，0）和B（0，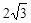
），线段AB的垂直平分线交x轴于点C，交AB于点D.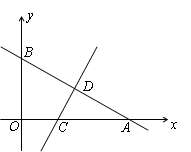
（1）试确定这个一次函数解析式；
（2）求过A、B、C三点的抛物线的函数关系式；
（3）请你利用所求抛物线的图像回答：当x取何值时，抛物线中的部分图像落在x轴的上方？
某市政府大力扶持大学生创业．李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y(件)与销售单价x(元)之间的关系可近似的看做一次函数：y＝－10x＋500.
（1）设李明每月获得利润为w(元)，当销售单价定为多少元时，每月可获得最大利润？
（2）如果李明想要每月获得2 000元的利润，那么销售单价应定为多少元？
（3）物价部门规定，这种护眼台灯的销售单价不得高于32元，如果李明想要每月获得的利润不低于2 000元，那么他每月的成本最少需要多少元？(成本＝进价×销售量)
抛物线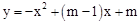
与y轴交于点（0，3）．
（1）求抛物线的解析式；
（2）求抛物线与坐标轴的交点坐标；
（3）① 当x取什么值时，y＞0 ？
② 当x取什么值时，y的值随x的增大而减小？
如图，等腰梯形ABCD放置在平面直角坐标系中，已知A（-2，0）、B（6，0）、A（0，3），反比例函数的图象经过点C．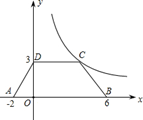
（1）求C点坐标和反比例函数的解析式；
（2）将等腰梯形ABCD向上平移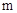
个单位后，使点B恰好落在双曲线上，求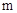的值．