如图甲,在的空间中存在沿轴负方向的匀强电场和垂直于平面向里的匀强磁场,电场强度大小为,磁感应强度大小为。一质量为,带电量为的粒子从坐标原点处,以初速度沿轴正方向射入,粒子的运动轨迹见图甲,不计粒子的重力。
⑴求该粒子运动到时的速度大小;
⑵现只改变入射粒子初速度的大小,发现初速度大小不同的粒子虽然运动轨迹(曲线)不同,但具有相同的空间周期性,如图乙所示;同时,这些粒子在轴方向上的运动(关系)是简谐运动,且都有相同的周期。
Ⅰ.求粒子在一个周期内,沿轴方向前进的距离;
Ⅱ.当入射粒子的初速度大小为时,其图像如图丙所示,求该粒子在轴方向上做简谐运动的振幅,并写出的函数表达式。
某人站在高楼的平台边缘处,以v0=20m/s的初速度竖直向上抛出一石子.求抛出后,石子经过距抛出点15m处所需的时间.(不计空气阻力,g取10m/s2)
如图所示,两足够长的光滑金属导轨竖直放置,相距为L,一理想电流表与两导轨相连,匀强磁场与导轨平面垂直.一质量为m、有效电阻为R的导体棒在距磁场上边界h处静止释放.导体棒进入磁场后,流经电流表的电流逐渐减小,最终稳定为I.整个运动过程中,导体棒与导轨接触良好,且始终保持水平,不计导轨的电阻.求: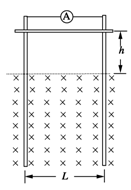
磁感应强度的大小B;
电流稳定后,导体棒运动速度的大小v;
流经电流表电流的最大值Im.
据报道,最近已研制出一种可以投入使用的电磁轨道炮,其原理如右图所示.炮弹(可视为长方形导体)置于两固定的平行导轨之间,并与轨道壁密接.开始时炮弹在导轨的一端,通电流后,炮弹会被磁场力加速,最后从位于导轨另一端的出口高速射出.设两导轨之间的距离d=0.10m,导轨长L=5.0m,炮弹质量m=0.30kg.导轨上的电流I的方向如图中箭头所示.可认为,炮弹在轨道内运动时,它所在处磁场的磁感应强度始终为B=2.0T,方向垂直于纸面向里.若炮弹出口速度为υ=2.0×103m/s,求通过导轨的电流I.(忽略摩擦力与重力的影响)
如右图所示,电源电动势E=10V,内阻r=1Ω,R1=3Ω,R2=6Ω,C=30μF.
闭合开关S,求稳定后通过R1的电流.
然后将开关S断开,求电容器两端的电压变化量和流过R1的总电量.
如果把R2换成一个可变电阻,其阻值可以在0~10Ω范围变化,求开关闭合并且电路稳定时,R2消耗的最大电功率.
如图所示,电荷量为-e,质量为m的电子从A点沿与电场线垂直的方向进入匀强电场,初速度为v0,当它通过电场B点时,速度与场强方向成150°角,不计电子的重力,求A、B两点间的电势差.