设f(x)是定义在[-1,1]上的奇函数,且对任意的实数a,b∈[-1,1],当a+b
≠0时,都有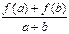 >0.
>0.
(1)若a>b,试比较f(a)与f(b)的大小;
(2)解不等式f(x -
- )<f(x-
)<f(x-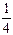 );
);
(3)如果g(x)=f(x-c)和h(x)=f(x-c2)这两个函数的定义域的交集是空集,求c的取值范围.
已知数列{an}的前n项和为Sn,且Sn=2n2+n,n∈N*,数列{bn}满足an=4log2bn+3,n∈N*.
(1)求an,bn;
(2)求数列{an·bn}的前n项和Tn.
设Sn为数列{an}的前n项和,已知a1≠0,2an-a1=S1·Sn,n∈N*.
(1)求a1,a2,并求数列{an}的通项公式;
(2)求数列{nan}的前n项和.
等差数列{an}中,a7=4,a19=2a9.
(1)求{an}的通项公式;
(2)设bn= ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.
设数列{an}满足a1=2,a2+a4=8,且对任意n∈N*,函数f(x)=(an-an+1+an+2)x+an+1cos x-an+2sin x满足f′ =0.
=0.
(1)求数列{an}的通项公式;
(2)若bn=2(an+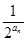 ),求数列{bn}的前n项和Sn.
),求数列{bn}的前n项和Sn.
设等差数列{an}的前n项和为Sn,且S4=4S2,a2n=2an+1.
(1)求数列{an}的通项公式;
(2)设数列{bn}满足 +
+ +…+
+…+ =1-
=1- ,n∈N* ,求{bn}的前n项和Tn.
,n∈N* ,求{bn}的前n项和Tn.