如图，在直三棱柱ABC-A1B1C1中，AC=3，BC=4，AB=5，AA1=4，点D是AB的中点.
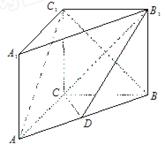
（1）求证：
∥平面
；
（2）求异面直线与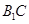
所成角的余弦值.
已知
展开式中的所有二项式系数和为512，
（1）求展开式中的常数项；
（2）求展开式中所有项的系数之和。
已知函数
（
且
）.
（1）当
时，求证:
在
上单调递增；
（2）当
且
时,求证:
.
曲线
，曲线
.自曲线
上一点
作
的两条切线切点分别为
.
（1）若点的纵坐标为
，求
；
（2）求
的最大值.
如图,已知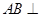
平面
,
为等边三角形.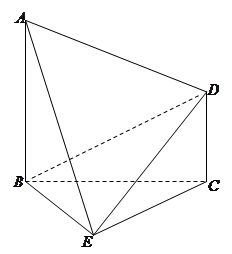
（1）若
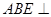，求证：平面
平面
；
（2）若多面体
的体积为
,求此时二面角
的余弦值.
在进行一项掷骰子放球游戏中，规定：若掷出1点，甲盒中放一球；
若掷出2点或3点，乙盒中放一球；若掷出4点或5点或6点，丙盒中放一球，前后共掷3
次，设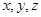
分别表示甲，乙，丙3个盒中的球数.
（1）求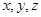依次成公差大于0的等差数列的概率；
（2）记
，求随机变量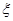
的概率分布列和数学期望.