如图,已知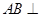 平面
平面 ,
, 为等边三角形.
为等边三角形.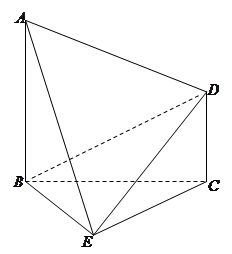
(1)若 ,求证:平面
,求证:平面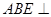 平面
平面 ;
;
(2)若多面体 的体积为
的体积为 ,求此时二面角
,求此时二面角 的余弦值.
的余弦值.
已知集合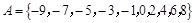 ,在平面直角坐标系中,点
,在平面直角坐标系中,点 的
的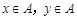 ,且
,且 ,计算
,计算
(1)点 不在x轴上的概率;
不在x轴上的概率;
(2)点 正好在第二象限的概率.
正好在第二象限的概率.
在箱子里装有10张卡片,分别写有1到10的10个数字,从箱子中任取一张卡片,记下它的读数x,然后再放回箱子中;第二次再从箱子中任意取出一张卡片,记下它的读数y.
求:(1) 是10的倍数的概率;
是10的倍数的概率;
(2)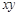 是3的倍数的概率.
是3的倍数的概率.
平面上画了一些彼此相距2a的平行线,把一枚半径r<a的硬币任意掷在这个平面上,求硬币不与任一条平行线相碰的概率.
一海豚在水池中自由游弋,水池为长30 m,宽20 m的长方形,求海豚嘴尖离岸边不超过2 m的概率.
在等腰Rt△ABC中,在斜边AB上任取一点M,求AM的长小于AC的长的概率.