(本小题满分12分)上海某玩具厂生产 套世博吉祥物“海宝”所需成本费用为
套世博吉祥物“海宝”所需成本费用为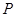 元,且
元,且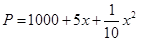 ,而每套“海宝”售出的价格为
,而每套“海宝”售出的价格为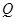 元,其中
元,其中
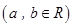 ,
,
(1)问:该玩具厂生产多少套“海宝”时,使得每套所需成本费用最少?
(2)若生产出的“海宝”能全部售出,且当产量为150套时利润最大,此时每套价格为30元,求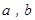 的值.(利润 = 销售收入-成本)
的值.(利润 = 销售收入-成本)
为了绿化城市,准备在如图所示的区域内修建一个矩形PQRC的草坪,且PQ//BC,RQ BC。另外
BC。另外 的内部有一文物保护区不能占用,经测量AB="100m," BC="80m," AE="30m," AF=20m,应如何设计才能使草坪的占地面积最大?
的内部有一文物保护区不能占用,经测量AB="100m," BC="80m," AE="30m," AF=20m,应如何设计才能使草坪的占地面积最大?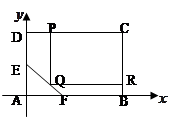
正三棱柱 中,E为AC中点
中,E为AC中点
(1)求证: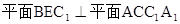
(2)求证: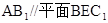 ,
,
已知直线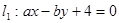 和直线
和直线 ,求分别满足下列条件的
,求分别满足下列条件的 的值
的值
(1) 直线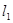 过点
过点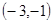 ,并且直线
,并且直线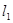 和
和 垂直
垂直
(2)直线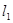 和
和 平行,且直线
平行,且直线 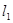 在
在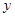 轴上的截距为-3
轴上的截距为-3
已知圆C的参数方程为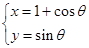 (
(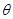 为参数),P是圆C与x轴的正半轴的交点.
为参数),P是圆C与x轴的正半轴的交点.
(1)求过点P的圆C的切线极坐标方程和圆C的极坐标方程;
(2)在圆C上求一点Q(a, b),它到直线x+y+3=0的距离最长,并求出最长距离。
已知椭圆C: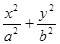 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为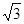 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l与椭圆C交于A、B两点,坐标原点O到直线l的距离为 ,求△AOB面积的最大值.
,求△AOB面积的最大值.