已知直线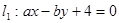 和直线
和直线 ,求分别满足下列条件的
,求分别满足下列条件的 的值
的值
(1) 直线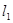 过点
过点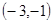 ,并且直线
,并且直线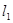 和
和 垂直
垂直
(2)直线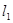 和
和 平行,且直线
平行,且直线 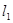 在
在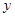 轴上的截距为-3
轴上的截距为-3
(本小题满分13分)某中学为丰富学生的业余生活,举行“汉字听写大会”,高一(1)班语文老师要求参赛学生从星期一到星期四每天学习3个汉字以及正确注释,每周五对一周内所学汉字随机抽取若干个进行检测(一周所学的汉字每个被抽到的可能性相同).
(Ⅰ)若从一周所学的汉字中,随机抽了4个汉字进行检测,求恰有3个是后两天学习过的汉字的概率;
(Ⅱ)高一(1)班学生小闽对周一、周二所学过的汉字每个能默写正确的概率为,对周三、周四所学过的汉字每个能默写对的概率为.若老师从后三天所学汉字中各抽取一个进行检测,求小闽能默写对的汉字的个数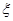 的分布列和期望.
的分布列和期望.
(本小题满分13分)如图,在四棱锥中,底面是正方形,底面,, 点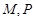 分别是
分别是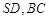 的中点,,且交于点.
的中点,,且交于点.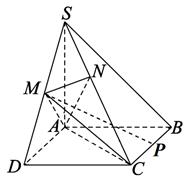
(Ⅰ)求证: 平面
平面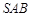 ;
;
(Ⅱ)求证:平面⊥平面;
(Ⅲ)求二面角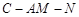 的余弦值.
的余弦值.
已知
(Ⅰ)求函数的最小正周期和对称中心;
(Ⅱ)将函数的图象向右平移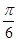 个单位,得到函数
个单位,得到函数 的图象,当时,方程
的图象,当时,方程 有实数解,求实数的取值范围.
有实数解,求实数的取值范围.
关于 的不等式
的不等式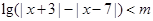 .
.
(Ⅰ)当 时,解此不等式;
时,解此不等式;
(Ⅱ)设函数 ,当
,当 为何值时,
为何值时, 恒成立?
恒成立?
已知曲线 的极坐标方程是
的极坐标方程是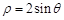 ,直线
,直线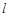 的参数方程是
的参数方程是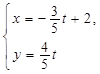 (
(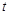 为参数).
为参数).
(Ⅰ)将曲线 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(Ⅱ)设直线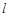 与
与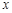 轴的交点是
轴的交点是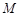 ,
, 是曲线
是曲线 上一动点,求
上一动点,求 的最大值.
的最大值.