(本小题满分12分)
数列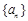 的前
的前 项和为
项和为 ,若
,若 ,点
,点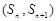 在直线
在直线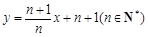 上.
上.
⑴求证:数列 是等差数列;
是等差数列;
⑵若数列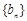 满足
满足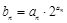 ,求数列
,求数列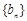 的前
的前 项和
项和 ;
;
⑶设 ,求证:
,求证: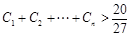 .
.
(本小题满分13分).某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为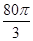 立方米,且
立方米,且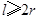 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为 千元,设该容器的建造费用为
千元,设该容器的建造费用为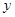 千元.
千元.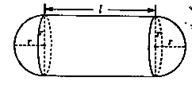
(Ⅰ)写出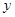 关于
关于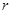 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(Ⅱ)求该容器的建造费用最小时的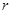 .
.
(本小题满分12分)如图,四棱锥P--ABCD中,PB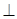 底面ABCD.底面ABCD为直角梯形,AD∥BC,AB=AD=PB=3,BC=6.点E在棱PA上,且PE=2EA.
底面ABCD.底面ABCD为直角梯形,AD∥BC,AB=AD=PB=3,BC=6.点E在棱PA上,且PE=2EA.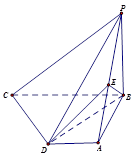
(1)求异面直线PA与CD所成的角;
(2)求证:PC∥平面EBD;
(3)求二面角A—BE--D的余弦值.
(本小题满分12分)
已知数列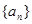 满足条件:
满足条件: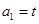 ,
,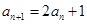
(1)判断数列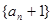 是否为等比数列;
是否为等比数列;
(2)若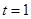 ,令
,令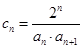 , 记
, 记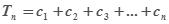
证明: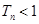
(本小题满分12分)本着健康、低碳的生活理念,租自行车骑游的人越来越多。某自行车租车点的收费标准是每车每次租不超过两小时免费,超过两小时的部分每小时收2元(不足1小时的部分按1小时计算)。有人独立来该租车点租车骑游。各租一车一次。设甲、乙不超过两小时还车的概率分别为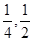 ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为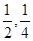 ;两人租车时间都不会超过四小时。
;两人租车时间都不会超过四小时。
(Ⅰ)求甲、乙两人所付租车费用相同的概率;
(Ⅱ)求甲、乙两人所付的租车费用之和为随机变量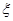 ,求
,求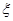 的分布列与数学期望
的分布列与数学期望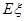 .
.
在平面直角坐标系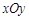 中,已知圆
中,已知圆 ,
,
圆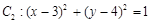 .
.
(Ⅰ)若过点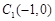 的直线
的直线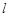 被圆
被圆 截得的弦长为
截得的弦长为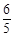 ,求直线
,求直线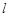 的方程;
的方程;
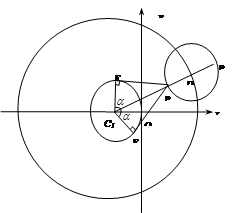
(Ⅱ)圆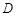 是以1为半径,圆心在圆
是以1为半径,圆心在圆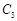 :
: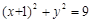 上移动的动圆 ,若圆
上移动的动圆 ,若圆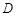 上任意一点
上任意一点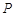 分别作圆
分别作圆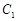 的两条切线
的两条切线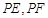 ,切点为
,切点为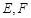 ,求
,求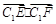 的取值范围 ;
的取值范围 ;
(Ⅲ)若动圆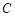 同时平分圆
同时平分圆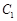 的周长、圆
的周长、圆 的周长,如图所示,则动圆
的周长,如图所示,则动圆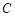 是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.