(本小题满分12分)本着健康、低碳的生活理念,租自行车骑游的人越来越多。某自行车租车点的收费标准是每车每次租不超过两小时免费,超过两小时的部分每小时收2元(不足1小时的部分按1小时计算)。有人独立来该租车点租车骑游。各租一车一次。设甲、乙不超过两小时还车的概率分别为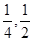 ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为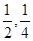 ;两人租车时间都不会超过四小时。
;两人租车时间都不会超过四小时。
(Ⅰ)求甲、乙两人所付租车费用相同的概率;
(Ⅱ)求甲、乙两人所付的租车费用之和为随机变量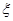 ,求
,求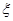 的分布列与数学期望
的分布列与数学期望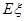 .
.
(本小题满分12分)
设二次函数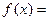
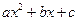 ,函数
,函数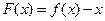 的两个零点为
的两个零点为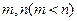 .
.
(1)若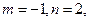 求不等式
求不等式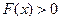 的解集;
的解集;
(2)若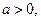 且
且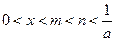 ,比较
,比较 与
与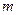 的大小.
的大小.
(本小题满分12 分)
分)
设椭圆C: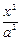 +
+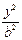 =1(a>b>0)的左焦点为F,过点F的直线与椭圆C相交于A,B两点,直线l的倾斜角为60°,
=1(a>b>0)的左焦点为F,过点F的直线与椭圆C相交于A,B两点,直线l的倾斜角为60°, AF=2
AF=2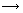 FB.
FB.
(I)求椭圆C的离心率;
(II)如果|AB|=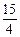 ,求椭圆C的方程.
,求椭圆C的方程.
(本小题满分12分)
已知函数f(x)=x2(x-3a)+1 (a>0,x∈R).
(a>0,x∈R).
(I)求函数y=f(x)的极值;
(II)函数y=f(x)在(0,2)上单调 递减,求实数a的取值范围;
递减,求实数a的取值范围;
(III)若在区间(0,+∞)上存在实数x0,使得不等式f(x0)-4a3≤0能成立,求实数a的取值范围.
(本小题满分12分)
某同学 参加3门课程的考试.假
参加3门课程的考试.假 设该同学第一门课程取得优秀成绩的概率为
设该同学第一门课程取得优秀成绩的概率为 ,第二、第三门课程取得优秀成绩的概率分别为p,q(p>q),且不同课程是否取得优秀成绩相互独立,记ξ为该生取得优秀成绩的课程数,其分布列为
,第二、第三门课程取得优秀成绩的概率分别为p,q(p>q),且不同课程是否取得优秀成绩相互独立,记ξ为该生取得优秀成绩的课程数,其分布列为
| ξ |
0 |
1 |
2 |
3 |
| p |
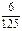 |
a |
b |
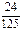 |
(I)求该生至少有1门课程取得优秀成绩的概率;
(II)求p,q的值;
(III)求数学期望Eξ.
(本小题满分12分)
如图,已知三棱锥P—ABC中,PA⊥平面ABC,
AB⊥AC,PA=AC= AB,N为AB
AB,N为AB 上一点,
上一点,
AB=4AN,M,S分别为PB,BC的中点.
(I)证明:CM⊥SN;
(II)求SN与平面CMN所成角的大小.