在如图所示的空间几何体中，平面
平面
，
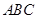是边长为2的等边三角形，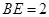
，
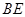和平面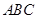所成的角为60°，且点
在平面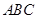上的射影落在
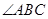的平分线上．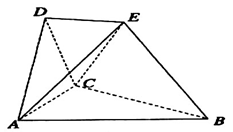
（1）求证：
//平面；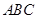
（2）求二面角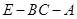
的余弦值．
已知抛物线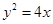
的焦点为F2，点F1与F2关于坐标原点对称，直线m垂直于x轴（垂足为T），与抛物线交于不同的两点P,Q且
.
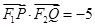（I）求点T的横坐标
；
（II）若以F1,F2为焦点的椭圆C过点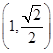
.
①求椭圆C的标准方程；
②过点F2作直线l与椭圆C交于A,B两点，设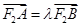
，若
的取值范围.
已知函数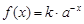
（
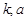为常数,
且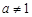
）的图象过点
.
（1）求实数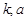的值;
（2）若函数
,试判断函数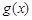
的奇偶性,并说明理由
某种商品，现在定价p元，每月卖出n件，设定价上涨x成，每月卖出数量减少y成，每月售货总金额变成现在的z倍．
(1)用x和y表示z；
(2)设x与y满足y＝kx(0<k<1)，利用k表示当每月售货总金额最大时x的值；
(3)若y＝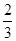
x，求使每月售货总金额有所增加的x值的范围．
已知单调递增的等比数列{an}满足a1+a2+a3=14，且a2+1是a1，a3的等差中项．
（1）求数列{an}的通项公式；
（2）若bn=anlog2an，求数列{bn}的前n项和Sn；
（3）若存在n∈N*，使得Sn+1﹣2≤8n3λ成立，求实数λ的最小值．
如图，在三棱柱ABC﹣A1B1C1中，AA1⊥底面ABC，且△ABC为正三角形，AA1=AB=6，D为AC的中点．
（1）求证：直线AB1∥平面BC1D；
（2）求证：平面BC1D⊥平面ACC1A；
（3）求三棱锥C﹣BC1D的体积．