已知抛物线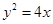
的焦点为F2，点F1与F2关于坐标原点对称，直线m垂直于x轴（垂足为T），与抛物线交于不同的两点P,Q且
.
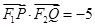（I）求点T的横坐标
；
（II）若以F1,F2为焦点的椭圆C过点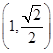
.
①求椭圆C的标准方程；
②过点F2作直线l与椭圆C交于A,B两点，设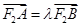
，若
的取值范围.
已知数列{an}，如果数列{bn}满足b1＝a1，bn＝an＋an－1，n≥2，n∈N*，则称数列{bn}是数列{an}的“生成数列”．
(1)若数列{an}的通项为an＝n，写出数列{an}的“生成数列”{bn}的通项公式；
(2)若数列{cn}的通项为cn＝2n＋b(其中b是常数)，试问数列{cn}的“生成数列”{qn}是否是等差数列，请说明理由；
(3)已知数列{dn}的通项为dn＝2n＋n，求数列{dn}的“生成数列”{pn}的前n项和Tn.
设正项数列{an}的前n项和为Sn，若{an}和{
}都是等差数列，且公差相等．
(1)求{an}的通项公式；
(2)若a1，a2，a5恰为等比数列{bn}的前三项，记数列cn＝
，数列{cn}的前n项和为Tn.求证：对任意n∈N*，都有Tn<2.
已知向量p＝(an,2n)，向量q＝(2n＋1，－an＋1)，n∈N*，向量p与q垂直，且a1＝1.
(1)求数列{an}的通项公式；
(2)若数列{bn}满足bn＝log2an＋1，求数列{an·bn}的前n项和Sn.
如图，在等腰直角△OPQ中，∠POQ＝90°，OP＝2
，点M在线段PQ上．
(1)若OM＝
，求PM的长；
(2)若点N在线段MQ上，且∠MON＝30°，问：当∠POM取何值时，△OMN的面积最小？并求出面积的最小值．
在△ABC中，角A，B，C的对边分别为a，b，c，若acos2
＋ccos2
＝
b.
(1)求证：a，b，c成等差数列；
(2)若∠B＝60°，b＝4，求△ABC的面积．