在平面直角坐标系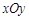 中,已知圆
中,已知圆 ,
,
圆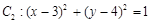 .
.
(Ⅰ)若过点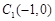 的直线
的直线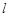 被圆
被圆 截得的弦长为
截得的弦长为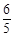 ,求直线
,求直线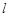 的方程;
的方程;
(Ⅱ)圆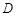 是以1为半径,圆心在圆
是以1为半径,圆心在圆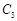 :
: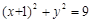 上移动的动圆 ,若圆
上移动的动圆 ,若圆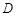 上任意一点
上任意一点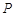 分别作圆
分别作圆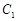 的两条切线
的两条切线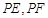 ,切点为
,切点为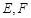 ,求
,求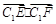 的取值范围 ;
的取值范围 ;
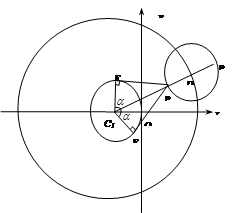
(Ⅲ)若动圆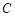 同时平分圆
同时平分圆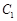 的周长、圆
的周长、圆 的周长,如图所示,则动圆
的周长,如图所示,则动圆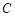 是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
(本小题满分12分)
已知某单位有50名职工,从中按系统抽样抽取10名职工,分别统计这10名职工的体重(单位:公斤),获得体重数据的茎叶图如图所示。
(Ⅰ)求该样本的方差;
(Ⅱ)从这10名职工中随机抽取两名体重不轻于73公斤的职工,求体重为76公斤的职工被抽取到的概率。
(本小题满分12分)
已知向量 ,
,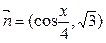 ,函数
,函数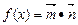 .
.
(Ⅰ)求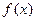 的最小正周期;
的最小正周期;
(Ⅱ)若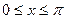 ,求
,求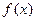 的最大值和最小值.
的最大值和最小值.
设函数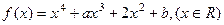 ,其中
,其中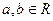
(1)当 时,讨论函数f(x)的单调性;
时,讨论函数f(x)的单调性;
(2)若函数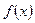 仅在
仅在 处有极值,求
处有极值,求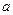 的取值范围;
的取值范围;
(3)若对于任意的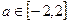 ,不等式
,不等式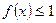 在[-1,1]上恒成立,求b的取值范围.
在[-1,1]上恒成立,求b的取值范围.
已知各项均为正数的数列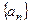 前
前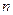 项和为
项和为 ,首项为
,首项为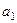 ,且
,且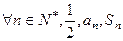 成等差数列.
成等差数列.
(1)求数列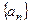 的通项公式;
的通项公式;
(2)若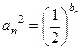 ,设
,设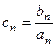 ,求数列
,求数列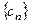 的前
的前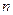 项和
项和 .
.
已知函数
 为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
(1)求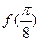 的值;
的值;
(2)将函数y=f(x)的图象向右平移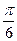 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.