一袋子中有大小相同的2个红球和3个黑球,从袋子里随机取球,取到每个球的可能性是相同的,设取到一个红球得2分,取到一个黑球得1分。(Ⅰ)若从袋子里一次随机取出3个球,求得4分的概率;(Ⅱ)若从袋子里每次摸出一个球,看清颜色后放回,连续摸3次,求得分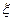 的概率分布列及数学期望。
的概率分布列及数学期望。
某校高三文科分为四个班.高三数学调研测试后, 随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人. 抽取出来的所有学生的测试成绩统计结果的频率分布条形图如所示,其中120~130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人. 0(1) 问各班被抽取的学生人数各为多少人?
(2) 在抽取的所有学生中,任取一名学生, 求分数不小于90分的概率.
有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表.
| 优秀 |
非优秀 |
总计 |
|
| 甲班 |
10 |
||
| 乙班 |
30 |
||
| 合计 |
105 |
已知在全部105人中抽到随机抽取1人为优秀的概率为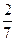
(Ⅰ)请完成上面的列联表;
(Ⅱ)根据列联表的数据,若按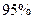 的可靠性要求,能否认为“成绩与班级有关系”.
的可靠性要求,能否认为“成绩与班级有关系”.
(Ⅲ)若按下面的方法从甲班优秀的学生抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到6或10号的概率.
某中学在高一开设了数学史等4门不同的选修课,每个学生必须选修,有只能从中选一门。该校高一的3名学生甲、乙、丙对这4门不同的选修课的兴趣相同。(Ⅰ)求3个学生选择了3门不同的选修课的概率;(Ⅱ)求恰有2门选修课这3个学生都没有选择的概率;(Ⅲ)设随机变量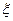 为甲、乙、丙这三个学生选修数学史这门课的人数,求
为甲、乙、丙这三个学生选修数学史这门课的人数,求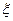 的分布列
的分布列
与数学期望。
某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:
| 日期 |
12月1日 |
12月2日 |
12月3日 |
12月4日 |
12月5日 |
温差 (°C) (°C) |
10 |
11 |
13 |
12 |
8 |
发芽数 (颗) (颗) |
23 |
25 |
30 |
26 |
16 |
该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.(1)求选取的2组数据恰好是不相邻2天数据的概率;(2)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求出y关于x的线性回归方程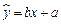 ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?