(12分)集合A是由具备下列性质的函数f(x)组成的:
①函数f(x)的定义域是[0,+∞);
②函数f(x)的值域是[-2,4);
③函数f(x)在[0,+∞)上是增函数,试分别探究下列两小题:
(1)判断函数f1(x)= -2(x≥0)及f2(x)=4-6·
-2(x≥0)及f2(x)=4-6· x(x≥0)是否属于集合A?并简要说明理由;
x(x≥0)是否属于集合A?并简要说明理由;
(2)对于(1)中你认为属于集合A的函数f(x),不等式f(x)+f(x+2)<2f(x+1)是否对于任意的x≥0恒成立?若不成立,为什么?若成立,请说明你的结论.
(本小题14分)
|
椭圆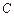 :
: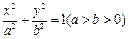 的离心率为
的离心率为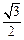 ,且过
,且过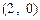 点.
点.
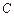 的方程;
的方程;
 :
: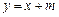 与椭圆
与椭圆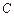 相交时,求m的取值范围;
相交时,求m的取值范围;
 :
: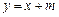 与椭圆
与椭圆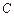 交于
交于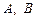 两点,
两点,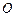 为坐标原点,若
为坐标原点,若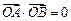 ,求
,求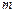 的值。
的值。
(本小题12分)
如图4:求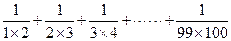 的算法的
的算法的
程序框图。⑴标号①处填。标号②处填。⑵根据框图用直到型(UNTIL)语句编写程序。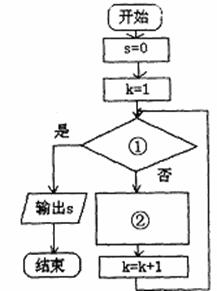
(本小题12分)
⑴焦点在y轴上的椭圆的一个顶点为A(2,0),其长轴长是短轴长的2倍,求椭圆的标准方程。
⑵已知双曲线的一条渐近线方程是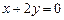 ,并经过点
,并经过点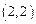 ,求此双曲线的标准方程。
,求此双曲线的标准方程。
(本小题12分)
甲、乙两位学生参加数学竞赛培训,在活动期间,他们参加的5次测试成绩记录如下:
甲 82 82 79 95 87乙 95 75 80 90 85
⑴用茎叶图表示这两组数据;
⑵若要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?说明理由。
(本小题12分)一个盒子中装有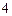 张卡片,每张卡片上写有
张卡片,每张卡片上写有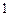 个数字,数字分别是
个数字,数字分别是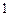 、
、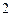 、
、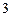 、
、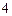 。现从盒子中随机抽取卡片,
。现从盒子中随机抽取卡片,
⑴若一次抽取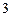 张卡片,求
张卡片,求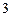 张卡片上数字之和大于
张卡片上数字之和大于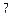 的概率;
的概率;
⑵若第一次抽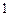 张卡片,放回后再抽取
张卡片,放回后再抽取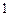 张卡片,求两次抽取中至少一次抽到数字
张卡片,求两次抽取中至少一次抽到数字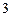 的概率。
的概率。