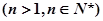（本小题满分12分）已知函数
．
（1）求f （x）的极值；
（2）已知
，设函数
的单调递减区间为
，且
，
函数
的单调递减区间为
，若
，求
的取值范围．
已知函数
.
(I)当a=3时，求曲线y=f(x)在点(1，f(1))处的切线方程；
(II)对任意b>0，f(x)在区间[b-lnb，+∞)上是增函数，求实数a的取值范围.
在平面四边形ABCD中，
ABC为正三角形，ADC为等腰直角三角形，AD=DC=2，将ABC沿AC折起，使点B至点P，且PD=2
，M为PA的中点，N在线段PD上。
(I)若PA
平面CMN，求证：AD//平面CMN；
(II)求直线PD与平面ACD所成角的余弦值。
己知等比数列{
}的公比为q，前n项和为Sn，且S1，S3，S2成等差数列．
(I)求公比q；
(II)若
，问数列{Tn}是否存在最大项?若存在，求出该项的值；若不存在，请说明理由。
ABC中内角A,B,C的对边分别为a，b，c，已知2a=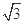
c,
．
(I)求
的值；
(II)若D为AC中点，且ABD的面积为
，求BD长。
已知函数
.
(1)求函数
的单调区间; (2)若
恒成立,求实数k的取值范围;
(3)证明: 
