已知点A,B分别是两条平行线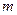 ,
,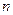 上任意两点,C是直线
上任意两点,C是直线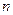 上一点,且
上一点,且
∠ABC=90°,点E在AC的延长线上,BC=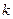 AB (k≠0).
AB (k≠0).
(1)当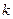 =1
=1 时,在图(1)中,作∠BEF=∠ABC,EF交直线
时,在图(1)中,作∠BEF=∠ABC,EF交直线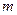 于点F.,写出线段EF与
于点F.,写出线段EF与
EB的数量关系,并加以证明;
(2)若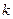 ≠1,如图(2),∠BEF=∠ABC,其它条件不变,探究线段EF与EB的数量关系,并说明理由.
≠1,如图(2),∠BEF=∠ABC,其它条件不变,探究线段EF与EB的数量关系,并说明理由.
(本题10分)已知AB为⊙O的直径,PA、PC是⊙O的切线,A、C为切点,∠BAC=30°.①求∠P的度数;②若AB=2,求PA的长.
(本题8分)如图, 是⊙
是⊙ 的切线,
的切线, 为切点,
为切点,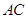 是⊙
是⊙ 的弦,过
的弦,过 作
作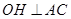 于点
于点 .若
.若 ,
, ,
, .
.
求:(1)⊙ 的半径;(2)AC的值.
的半径;(2)AC的值.
(本题8分)长沙市某楼盘准备以每平方米5000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望.为了加快资金周转,房地产开发商对价格经过两次下调后,决定以每平方米4050元的均价开盘销售.求平均每次下调的百分率.
(本题4分)右图是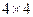 的正方形网格,请在其中选取一个白色的单位正方形并涂黑,使图中黑色部分是一个中心对称图形.
的正方形网格,请在其中选取一个白色的单位正方形并涂黑,使图中黑色部分是一个中心对称图形.
已知:如图①,四边形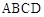 是正方形,
是正方形, 是等边三角形,
是等边三角形,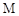 为对角线
为对角线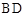 (不含
(不含 点)上任意一点,将
点)上任意一点,将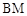 绕点
绕点 逆时针旋转
逆时针旋转 得到
得到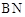 ,连接
,连接 、
、 、
、 。
。
(I)求证:
(II)①当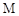 点在何处时,
点在何处时, 的值最小;
的值最小;
②当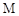 点在何处时,
点在何处时, 的值最小,并说明理由;
的值最小,并说明理由;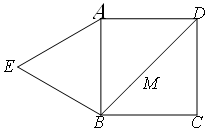
(III)当 的最小值为
的最小值为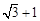 时,求正方形的边长。
时,求正方形的边长。