(本题8分)长沙市某楼盘准备以每平方米5000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望.为了加快资金周转,房地产开发商对价格经过两次下调后,决定以每平方米4050元的均价开盘销售.求平均每次下调的百分率.
(1)已知:线段a,∠α.求作:△ABC,使BC=a,∠C=∠B=∠α.(不写作法,保留作图痕迹)
(2)在(1)的图形中,如果BC=6 ,∠α=30°,求△ABC的面积.
,∠α=30°,求△ABC的面积.
先化简,再求值:(x+5)(x-1)+(x-2)2,其中x=- .
.
(1)问题发现:
如图1,点A、B是直线l外的任意两点,在直线l上,试确定一点P,使PA,PB最短.
作法如下:作点A关于直线l的对称点A′,连结A′B交l于点P,则PA+PB=A′B最短.(不必证明)
(2)解决问题:
如图2,等边△ABC的边长为4,E为AB的中点,AD⊥BC,P是AD上一点.
①在图中画出点P,使点B,E到点P的距离之和最短;(保留作图痕迹,不写作法)
②求这个最短距离.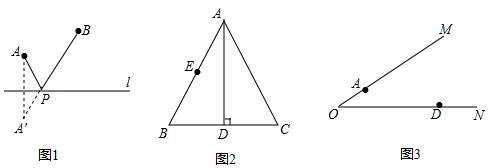
(3)应用拓展:如图3,角形铁架∠MON=30°,A,D分别是OM,ON上的定点,且OA=7,OD=24,为实际设计的需要,需在OM和ON上分别找出点C,B,使AB+BC+CD的值最小.请在图中画出点B、C,则此时的最小值为 (保留作图痕迹,不写作法)
某文化用品商店用2000元购进一批学生书包,面市后发现供不应求,商店又购进第二批同样的书包,所购数量是第一批购进数量的3倍,但单价贵了4元,结果第二批用了6300元.
(1)求第一批购进书包的单价是多少元?
(2)若商店销售这两批书包时,每个售价都是120元,全部售出后,商店共盈利多少元?
数学课上,探讨角平分线的作法时,小明发现只利用直角三角板也可以作角平分线,操作如下: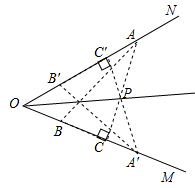
①先让三角板的直角边BC落在OM上,使顶点A恰好落在ON上;
②按上述操作,再将该三角板放置到如图所示的△A′B′C′的位置,B′C′落在ON上,顶点A′落在OM上,AC与A′C′交于点P;
③作射线OP,则OP就是∠MON的平分线.
(1)小明在推证其作法正确性的过程中,仅得出△OAC≌△OA′C′,则这两个三角形全等的依据是 ;
(2)在(1)的基础上,请你帮助小明继续完成证明过程.