(1)问题发现:
如图1,点A、B是直线l外的任意两点,在直线l上,试确定一点P,使PA,PB最短.
作法如下:作点A关于直线l的对称点A′,连结A′B交l于点P,则PA+PB=A′B最短.(不必证明)
(2)解决问题:
如图2,等边△ABC的边长为4,E为AB的中点,AD⊥BC,P是AD上一点.
①在图中画出点P,使点B,E到点P的距离之和最短;(保留作图痕迹,不写作法)
②求这个最短距离.
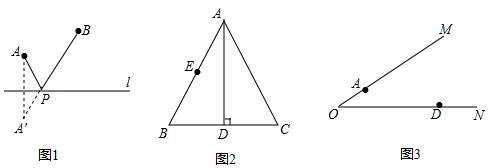
(3)应用拓展:如图3,角形铁架∠MON=30°,A,D分别是OM,ON上的定点,且OA=7,OD=24,为实际设计的需要,需在OM和ON上分别找出点C,B,使AB+BC+CD的值最小.请在图中画出点B、C,则此时的最小值为 (保留作图痕迹,不写作法)
五一期间某校组织七、八年级的同学到某景点郊游,该景点的门票全票票价为15元/人,若为50~99人可以八折购票,100人以上则可六折购票.已知参加郊游的七年级同学少于50人、八年级同学少于100人.若七、八年级分别购票,两个年级共计应付门票费1575元,若合在一起购买折扣票,总计应付门票费1080元.
(1)请你判断参加郊游的八年级同学是否也少于50人.
(2)求参加郊游的七、八年级同学各为多少人?
如图所示,已知在平行四边形ABCD中,BE=DF,求证:AE=CF.
如图,AB=AE,∠1=∠2,∠C=∠D.求证:△ABC≌△AED.
(1)化简: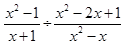 .
.
(2)解方程: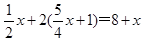 .
.
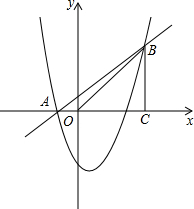
如图,已知抛物线y=x2+bx+c经过A(-1,0)、B(4,5)两点,过点B作BC⊥x轴,垂足为C.
(1)求抛物线的解析式;
(2)求tan∠ABO的值;
(3)点M是抛物线上的一个点,直线MN平行于y轴交直线AB于N,如果以M、N、B、C为顶点的四边形是平行四边形,求出点M的横坐标.