先阅读下面的解题过程，然后再解答：
形如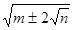
的化简，只要我们找到两个数
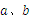，使
，
，即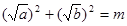
，
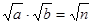，那么便有：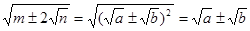
.
例如：化简：
.
解：首先把化为
，这里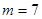
，
，
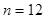由于
，
，
即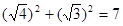
，
，
所以
.
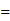
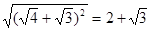根据上述方法化简：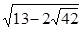
.
500多年前，数学各学派的学者都认为世界上的数只有整数和分数，直到有一天，大数学家毕达哥拉斯的一个名叫希帕索斯的学生，在研究1和2的比例中项时（若1∶x=x∶2，那么x叫1和2的比例中项)，他怎么也想不出这个比例中项值.后来，他画了一个边长为1的正方形，设对角线为x，于是由毕达哥拉斯定理x2=12+12=2,他想x代表对角线的长，而x2=2，那么x必定是确定的数，这时他又为自己提出了几个问题：
（1）x是整数吗？为什么不是？
（2）x可能是分数吗？是，能找出来吗？不是，能说出理由吗？亲爱的同学，你能帮他解答这些问题吗？
阅读下列解题过程：已知a，b，c为△ABC的三边，且满足a2c2－b2c2=a4－b4，试判定△ABC的形状.
解：∵a2c2－b2c2=a4－b4 ①
∴c2(a2－b2)=(a2+b2)(a2－b2) ②
∴c2=a2+b2③
∴△ABC是直角三角形
问：上述解题过程，从哪一步开始出现错误？
请写出该步的序号：_________；
错误的原因为_________；
本题正确的结论是_________.
已知a，b，c为△ABC三边，且满足a2+b2+c2+338=10a+24b+26c.试判断△ABC的形状.
阅读下列解题过程：已知a，b，c为△ABC的三边，且满足a2c2－b2c2=a4－b4，试判定△ABC的形状.
解：∵a2c2－b2c2=a4－b4 ①
∴c2(a2－b2)=(a2+b2)(a2－b2) ②
∴c2=a2+b2③
∴△ABC是直角三角形
问：上述解题过程，从哪一步开始出现错误？
请写出该步的序号：_________；
错误的原因为_________；
本题正确的结论是_________.
已知a，b，c为△ABC三边，且满足a2+b2+c2+338=10a+24b+26c.试判断△ABC的形状.