列方程或方程组解应用题:
我区教委要求各学校师生开展“彩虹读书活动”. 某校九年级一班和九年级二班的学生向学校图书馆借课外读物共196本，一班为每位学生借3本，二班为每位学生借2本，一班借的课外读物数量比二班借的课外读物数量多44本，求九年级一班和二班各有学生多少人？
如图，在梯形ABCD中，AD∥BC，∠B=90°，∠C=45°，AD=1，BC=4，E为AB中点，EF∥DC交BC于点F，求EF的长．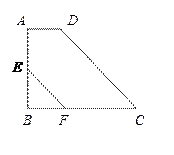
已知：关于x的一元二次方程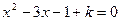
有两个不相等的实数根．
（1）求k的取值范围；
（2）请选择一个k的正整数值，并求出方程的根．
(本题满分8分)
已知：如图,四边形ABCD是平行四边形,△ADE和△BCF都是
等边三角形.
求证:BD和EF互相平分. 
用适当的方法解下列方程
（1）
(用配方法) （2）3x(x－1)=2－2x
已知等边△ABC和Rt△DEF按如图所示的位置放置，点B，D重合，且点Ｅ、B(D)、
C在同一条直线上．其中∠E=90°, 
,
，现将△DEF
沿直线BC以每秒
个单位向右平移，直至E点与C 点重合时停止运动，设运动时
间为t秒．
(1) 试求出在平移过程中，点F落在△ABC的边上时的t值；
(2) 试求出在平移过程中△ABC和Rt△DEF重叠部分的面积s与t的函数关系式；
(3) 当D与C重合时，点H为直线DF上一动点，现将△DBH绕点D顺时针旋转60°得到
△ACK，则是否存在点H使得△BHK的面积为
，若存在，试求出CH的值；若不存在，请说明理由．
