已知:如图,等边△ABC中,点D为BC边的中点,点F是AB边上一点,点E在线段DF的延长线上,∠BAE=∠BDF,点M在线段DF上,∠ABE=∠DBM.
(1)猜想:线段AE、MD之间有怎样的数量关系,并加以证明;
(2)在(1)的条件下延长BM到P,使MP=BM,连接CP,若AB=7,AE=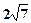 ,求tan∠BCP的值.
,求tan∠BCP的值.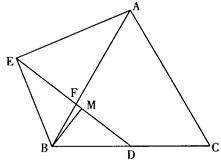
已知点A(3,4),点B为直线x=-1上的动点,设B(-1,y).
(1)如图1,若点C(x,0)且-1<x<3,BC⊥AC,求y与x之间的函数关系式;
(2)在(1)的条件下,y是否有最大值?若有,请求出最大值;若没有,请说明理由;
(3)如图2,当点B的坐标为(-1,1)时,在x轴上另取两点E,F,且EF=1.线段EF在x轴上平移,线段EF平移至何处时,四边形ABEF的周长最小?求出此时点E的坐标.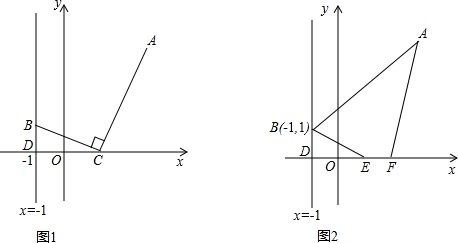
如图,已知矩形纸片ABCD,AD=2,AB=4.将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AB,CD交于点G,F,AE与FG交于点O.
(1)如图1,求证:A,G,E,F四点围成的四边形是菱形;
(2)如图2,当△AED的外接圆与BC相切于点N时,求证:点N是线段BC的中点;
(3)如图2,在(2)的条件下,求折痕FG的长.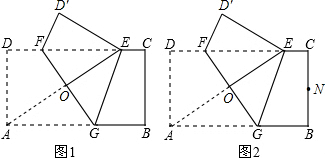
南宁市某生态示范村种植基地计划用90亩~120亩的土地种植一批葡萄,原计划总产量要达到36万斤.
(1)列出原计划种植亩数y(亩)与平均每亩产量x(万斤)之间的函数关系式,并写出自变量x的取值范围;
(2)为了满足市场需求,现决定改良葡萄品种.改良后平均每亩产量是原计划的1.5倍,总产量比原计划增加了9万斤,种植亩数减少了20亩,原计划和改良后的平均每亩产量各是多少万斤?
如图,山坡上有一棵树AB,树底部B点到山脚C点的距离BC为 米,山坡的坡角为30°.小宁在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
米,山坡的坡角为30°.小宁在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)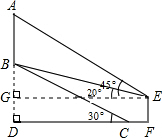
如图所示,∠BAC=∠ABD=90°,AC=BD,点O是AD,BC的交点,点E是AB的中点.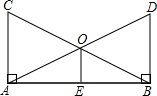
(1)图中有哪几对全等三角形?请写出来;
(2)试判断OE和AB的位置关系,并给予证明.