南宁市某生态示范村种植基地计划用90亩~120亩的土地种植一批葡萄,原计划总产量要达到36万斤.
(1)列出原计划种植亩数y(亩)与平均每亩产量x(万斤)之间的函数关系式,并写出自变量x的取值范围;
(2)为了满足市场需求,现决定改良葡萄品种.改良后平均每亩产量是原计划的1.5倍,总产量比原计划增加了9万斤,种植亩数减少了20亩,原计划和改良后的平均每亩产量各是多少万斤?
我校准备挑选一名跳高运动员参加区中学生运动会,对跳高队的甲、乙两名运动员进行了8次选拔比赛,他们的成绩(单位:cm)如下:
甲:170 165 168 169 172 173 168 167
乙:160 173 172 161 162 171 170 175甲、乙两名运动员的跳高平均成绩分别是多少?
哪名运动员的成绩更为稳定?为什么?
若预测,跳过165cm就很可能获得冠军。该校为了获得冠军,可能选哪位运动员参赛?若预测跳过170cm才能得冠军呢?为什么?
如图,在长方形ABCD中,,AB=6cm,BC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在点E处,BE交AD于点F,
求证:△FBD是等腰三角形;
求AF长。
如图,在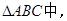
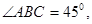 H是高AD、BE的交点,若BH=10,求AC的长
H是高AD、BE的交点,若BH=10,求AC的长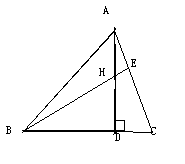
如图1,已知抛物线的顶点为 ,且经过原点
,且经过原点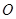 ,与
,与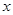 轴的另一个交点为
轴的另一个交点为 .
.求抛物线的解析式;
若
 点
点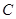 在抛物线的对称轴上,点
在抛物线的对称轴上,点 在抛物线上,且以
在抛物线上,且以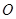 、
、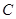 、
、 、
、 四点为
四点为 顶点的四边形为平行四边形,求
顶点的四边形为平行四边形,求 点的坐标;
点的坐标;连接
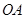 、
、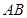 ,如图2,在
,如图2,在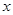 轴下方的抛物线上是否存在点
轴下方的抛物线上是否存在点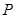 ,使得
,使得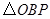 与
与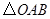 相似?若存在,求出
相似?若存在,求出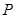 点的坐标;若不存在,说明理由.
点的坐标;若不存在,说明理由.
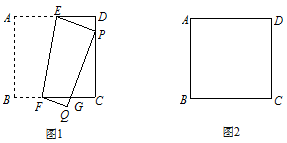
已知正方形纸片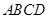 的边长为2.操作:如图1,将正方形纸片折叠,使顶点
的边长为2.操作:如图1,将正方形纸片折叠,使顶点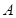 落在边
落在边 上的点
上的点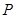 处(点
处(点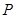 与
与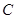 、
、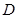 不重合),折痕为
不重合),折痕为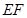 ,折叠后
,折叠后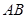 边落在
边落在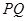 的位置,
的位置,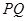 与
与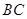 交于点
交于点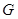 .
.
探究:观察操作结果,找到一个与
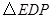 相似的三角形,并证明你的结论;
相似的三角形,并证明你的结论;当点
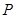 位于
位于 中点时,你找到的三角形与
中点时,你找到的三角形与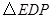 周长的比是多少(图2为备用图)?
周长的比是多少(图2为备用图)?