（1）在遇到问题：“钟
面上，如果把时针与分针看作是同一平面内的两条线段，在2∶00~2
∶15之间，时针与分针重合的时刻是多少？”时，小明尝试运用建立函数关系的方法：
①恰当选取变量x和y．小明设2点钟之后经过x min（0≤x≤15），时针、分针分别与竖轴线（即经过表示“12”和“6”的点的直线，如图1）所成的角的度数为y1°、y2°；
②确定函数关系．由于时针、分针在单位时间内转动的角度不变，因此既可以直接写出y1、y2关于x的函数关系式，也可以画出它们的图象．小明选择了后者，画出了图2；
③根据题目的要求，利用函数求解．本题中小明认为求出两个图象交点的横坐标就可以解决问题．
请你按照小明的思路解决这个问题．
（2）请运用建立函数关系的方法解决问题：钟面上，如果把时针与分针看作是同一平面
内
的两条线段，在7∶30~8∶00之间，时针与分针互相垂直的时刻是多少？
（·黑龙江哈尔滨）（本题10分）如图，在平面直角坐标系中，点O为坐标原点，直线y=kx+1（k≠0）与x轴交于点A，与y轴交于点C，过点C的抛物线y=ax2-（6a-2）x+b （a≠0）与直线AC交于另一点B，点B坐标为（4，3）．
（1）求a的值；
（2）点p是射线CB上的一个动点，过点P在作PQ⊥x轴，垂足为点Q，在x轴上点Q的右侧取点M，使MQ=
，在QP的延长线上取点N，连接PM，AN，已知tan∠NAQ-tan∠MPQ=
，求线段PN的长；
（3）在（2）的条件下，过点C作CD⊥AB，使点D在直线AB 下方，且CD=AC，连接PD，NC，当以PN，PD，NC的长为三边长构成的三角形面积是
时，在y轴左侧的抛物线上是否存在点E，连接NE，PE，使得ΔENP与以PN、PD、NC的长为三边长的三角形全等？若存在，求出点E坐标；若不存在，请说明理由．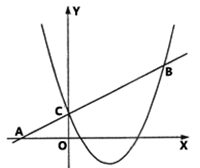
（·辽宁葫芦岛）如图，直线
与x轴交于点C，与y轴交于点B，抛物线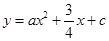
经过B、C两点．
（1）求抛物线的解析式；
（2）如图，点E是直线BC上方抛物线上的一动点，当△BEC面积最大时，请求出点E的坐标和△BEC面积的最大值？
（3）在（2）的结论下，过点E作y轴的平行线交直线BC于点M，连接AM，点Q是抛物线对称轴上的动点，在抛物线上是否存在点P，使得以P、Q、A、M为顶点的四边形是平行四边形？如果存在，请直接写出点P的坐标；如果不存在，请说明理由．
（·辽宁葫芦岛）在△ABC中，AB=AC，点F是BC延长线上一点，以CF为边，作菱形CDEF，使菱形CDEF与点A在BC的同侧，连接BE，点G是BE的中点，连接AG、DG．
（1）如图①，当∠BAC=∠DCF=90°时，直接写出AG与DG的位置和数量关系；
（2）如图②，当∠BAC=∠DCF=60°时，试探究AG与DG的位置和数量关系，
（3）当∠BAC=∠DCF=α时，直接写出AG与DG的数量关系．
（·辽宁沈阳）如图，在平面直角坐标系中，抛物线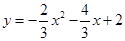
与x轴交于B、C两点（点B在点C的左侧），与y轴交于点A，抛物线的顶点为D．
（1）填空：点A的坐标为（， ），点B的坐标为（， ），点C的坐标为（， ），点D的坐标为（， ）；
（2）点P是线段BC上的动点（点P不与点B、C重合）
①过点P作x轴的垂线交抛物线于点E，若PE=PC，求点E的坐标；
②在①的条件下，点F是坐标轴上的点，且点F到EA和ED的距离相等，请直接写出线段EF的长；
③若点Q是线段AB上的动点（点Q不与点A、B重合），点R是线段AC上的动点（点R不与点A、C重合），请直接写出△PQR周长的最小值．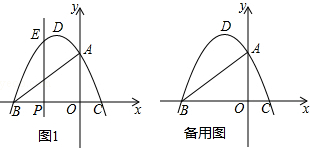
（·辽宁沈阳）如图，在▱ABCD中，AB=6，BC=4，∠B=60°，点E是边AB上的一点，点F是边CD上一点，将▱ABCD沿EF折叠，得到四边形EFGH，点A的对应点为点H，点D的对应点为点G．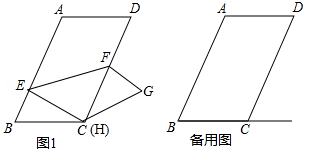
（1）当点H与点C重合时．
①填空：点E到CD的距离是 ；
②求证：△BCE≌△GCF；
③求△CEF的面积；
（2）当点H落在射线BC上，且CH=1时，直线EH与直线CD交于点M，请直接写出△MEF的面积．