（·黑龙江哈尔滨）（本题10分）如图，在平面直角坐标系中，点O为坐标原点，直线y=kx+1（k≠0）与x轴交于点A，与y轴交于点C，过点C的抛物线y=ax2-（6a-2）x+b （a≠0）与直线AC交于另一点B，点B坐标为（4，3）．
（1）求a的值；
（2）点p是射线CB上的一个动点，过点P在作PQ⊥x轴，垂足为点Q，在x轴上点Q的右侧取点M，使MQ=
，在QP的延长线上取点N，连接PM，AN，已知tan∠NAQ-tan∠MPQ=
，求线段PN的长；
（3）在（2）的条件下，过点C作CD⊥AB，使点D在直线AB 下方，且CD=AC，连接PD，NC，当以PN，PD，NC的长为三边长构成的三角形面积是
时，在y轴左侧的抛物线上是否存在点E，连接NE，PE，使得ΔENP与以PN、PD、NC的长为三边长的三角形全等？若存在，求出点E坐标；若不存在，请说明理由．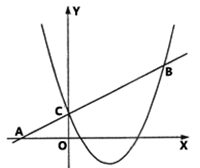
计算：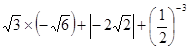
如图，在四边形ABCD中，点E、F是BC、CD的中点，且AE⊥BC，AF⊥CD．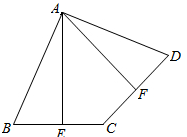
（1）求证：AB=AD．
（2）请你探究∠EAF，∠BAE，∠DAF之间有什么数量关系？并证明你的结论．
数学课上，探讨角平分线的作法时，李老师用直尺和圆规作角平分线，方法如下：
小颖的身边只有刻度尺，经过尝试，她发现利用刻度尺也可以作角平分线．
根据以上情境，解决下列问题：
①李老师用尺规作角平分线时，用到的三角形全等的判定方法是_________．
②小聪的作法正确吗？请说明理由．
③请你帮小颖设计用刻度尺作角平分线的方法．（要求：作出图形，写出作图步骤，不予证明）
解方程：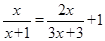
．
计算：
（1）
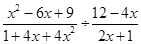
（2）
．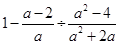