如图,PA与⊙O相切于A点,弦AB⊥OP,垂足为C,OP与⊙O相交于D点,已知OA=2,OP=4。
(1)求∠POA的度数;
(2)计算弦AB的长。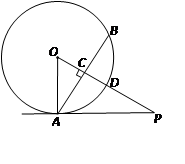
如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D、E两点的坐标.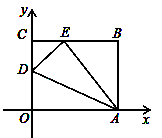
如图,已知:在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD.图中的CE、BD有怎样的大小和位置关系?试证明你的结论.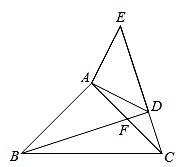
在同一直角坐标系中分别描出点A(-3,0)、B(2,0)、C(1,3),再用线段将这三点首尾顺次连接起来,求△ABC的面积与周长.
如图,已知∠AOB=30°,P为其内部一点,OP=3,M、N分别为OA、OB边上的一点,要使△PMN的周长最小,请给出确定点M、N位置的方法,并求出最小周长.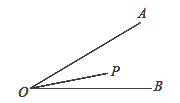
利用网格线画图:如图,点A、B、C都在正方形网格的格点上.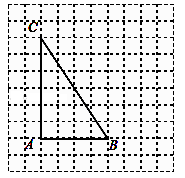
(1)在BC上找一点P,使PA=PB;
(2)在BC上找一点Q,使点Q到AB和AC的距离相等.