先观察下列等式,然后用你发现的规律解答下列问题.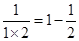 ;
; 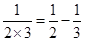 ;
; 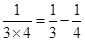 ; ┅┅
; ┅┅
(1) 计算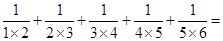 .
.
(2)探究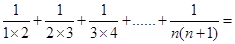 .(用含有
.(用含有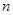 的式子表示)
的式子表示)
(3)若 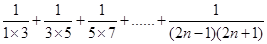 的值为
的值为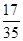 ,求
,求 的值.
的值.
已知:在Rt△ABC中,∠C=90°, ,
, ,解这个直角三角形.
,解这个直角三角形.
已知抛物线 用配方法求出它的顶点坐标、对称轴.
用配方法求出它的顶点坐标、对称轴.
.抛物线 与
与 轴交于A,B两点,与
轴交于A,B两点,与 轴交于C点,且A(
轴交于C点,且A( ,0)。
,0)。
(1)求抛物线的解析式及顶点坐标D的坐标;
(2)判断
 的形状,证明你的结论;
的形状,证明你的结论;(3)点M(m,0)是
 轴上的一个动点,当MC+MD的值最小时,求m的值。
轴上的一个动点,当MC+MD的值最小时,求m的值。
.某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
如图,已知梯形ABCD中,AB//CD,AB="2,CD=5," ∠ABC=90°,E是BC上一点,若把△CDE沿折痕折过去,C点恰好与A重合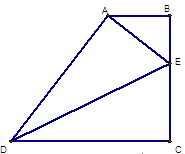
求:(1)BC的长
(2)tan∠CDE的值