已知
 .
.
(1)当 时,求
时,求 上的值域;
上的值域;
(2) 求函数 在
在 上的最小值;
上的最小值;
(3) 证明: 对一切 ,都有
,都有 成立
成立
(本小题满分12分)
△ABC中,a,b,c分别是角A,B,C的对边,向量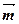 =(2sinB,2-cos2B),
=(2sinB,2-cos2B),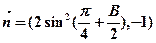 ,
,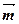 ⊥
⊥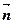 .
.
(1)求角B的大小;
(2)若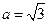 ,b=1,求c的值.
,b=1,求c的值.
(本小题满分12分)
在各项均为负数的数列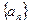 中,已知点
中,已知点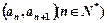 在函数
在函数 的图像上,且
的图像上,且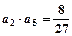 .
.
(1)求证:数列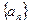 是等比数列,并求出其通项;
是等比数列,并求出其通项;
(2)若数列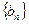 的前
的前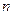 项和为
项和为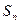 ,且
,且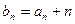 ,求
,求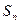 .
.
已知双曲线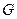 的中心在原点,它的渐近线与圆
的中心在原点,它的渐近线与圆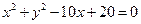 相切. 过点
相切. 过点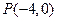 作斜率为
作斜率为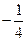 的直线
的直线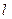 ,使
,使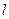 和
和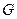 交于
交于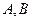 两点,和
两点,和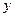 轴交于
轴交于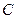 点,且点
点,且点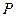 在线段
在线段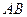 上,满足
上,满足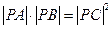
(I)求双曲线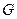 的渐近线方程;
的渐近线方程;
(II)求双曲线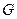 的方程;
的方程;
(Ⅲ)椭圆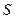 的中心在原点,它的短轴是
的中心在原点,它的短轴是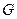 的实轴. 若
的实轴. 若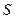 中垂直于
中垂直于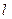 的平行弦的中点的轨迹恰好是
的平行弦的中点的轨迹恰好是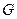 的渐近线截在
的渐近线截在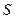 内的部分,求椭圆
内的部分,求椭圆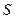 的方程.
的方程.
椭圆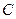 :
: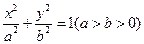 的离心率为
的离心率为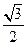 ,长轴端点与短轴端点间的距离为
,长轴端点与短轴端点间的距离为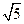 .
.
(I)求椭圆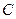 的方程;
的方程;
(II)设过点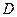
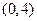 的直线
的直线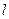 与椭圆
与椭圆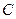 交于
交于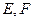 两点,
两点,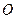 为坐标原点,若
为坐标原点,若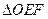 为直角三角形,求直线
为直角三角形,求直线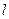 的斜率.
的斜率.
给定抛物线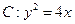 ,
,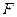 是抛物线
是抛物线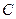 的焦点,过
的焦点,过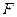 的直线
的直线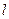 与
与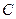 相交于
相交于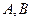 两点.
两点.
(1)设直线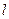 的斜率为1,求以
的斜率为1,求以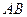 为直径的圆的方程;
为直径的圆的方程;
(2)若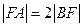 ,求直线
,求直线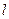 的方程.
的方程.