已知抛物线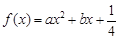 的最低点为
的最低点为 ,
,
(1)求不等式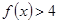 的解集;
的解集;
(2)若对任意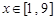 ,不等式
,不等式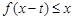 恒成立,求实数
恒成立,求实数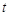 的取值范围.
的取值范围.
已知函数 ,
, 其中
其中
(Ⅰ)若 是函数
是函数 的极值点,求实数
的极值点,求实数 的值;
的值;
(Ⅱ)若对任意的 (
( 为自然对数的底数)都有
为自然对数的底数)都有 成立,求实数
成立,求实数 的取值范围
的取值范围
在平面直角坐标系 中,已知圆心在
中,已知圆心在 轴上,半径为
轴上,半径为 的圆
的圆 位于
位于 轴的右侧,且与
轴的右侧,且与 轴相切,
轴相切,
(Ⅰ)求圆 的方程;
的方程;
(Ⅱ)若椭圆 的离心率为
的离心率为 ,且左右焦点为
,且左右焦点为 ,试探究在圆
,试探究在圆 上是否存在点
上是否存在点 ,使得
,使得 为直角三角形?若存在,请指出共有几个这样的
为直角三角形?若存在,请指出共有几个这样的 点?并说明理由(不必具体求出这些点的坐标)
点?并说明理由(不必具体求出这些点的坐标)
为了调查学生的视力情况,随机抽查了一部分学生的视力,将调查结果分组,分组区间为 ,经过数据处理,得到如下频率分布表
,经过数据处理,得到如下频率分布表
| 分组 |
频数 |
频率 |
 |
3 |
0.06 |
 |
6 |
0.12 |
 |
25 |
 |
 |
 |
 |
 |
2 |
0.04 |
| 合计 |
 |
1.00 |
(Ⅰ)求频率分布表中未知量 ,
, ,
, ,
, 的值
的值
(Ⅱ)从样本中视力在 和
和 的所有同学中随机抽取两人,求两人视力差的绝对值低于
的所有同学中随机抽取两人,求两人视力差的绝对值低于 的概率
的概率
()如图,四棱锥 中,
中, 平面
平面 ,底面
,底面 是平行四边形,
是平行四边形, ,
,
 是
是 的中点
的中点
(Ⅰ)求证:
(Ⅱ)试在线段 上确定一点
上确定一点 ,使
,使 ,求三棱锥
,求三棱锥 的体积.
的体积.
在△ABC中, 分别为角
分别为角 所对的三边,已知
所对的三边,已知
(Ⅰ)求 的值
的值
(Ⅱ)若 ,求边
,求边 的长.
的长.